Kvadratiska former

Facit har gjort fel, men du har missat i matrismultiplikationen, så din matris stämmer inte heller.

Det ser ut som du multiplicerar matrisen med 2 istället för 1/2 på näst sista raden.

Men du tänker helt rätt. 

jamolettin skrev:

Facit har gjort fel, men du har missat i matrismultiplikationen, så din matris stämmer inte heller.

Det ser ut som du multiplicerar matrisen med 2 istället för 1/2 på näst sista raden.

Men du tänker helt rätt. 

Whoops du har rätt, har råkat göra fel. Men är du säker på att facit har fel?

Enligt mitt vetande, ja. 

Vi hade denna fråga i en tidigare tråd.

Fast matrisen måste ju vara ortogonal. Dvs både ortogonala kolumner och normerade kolumner.

Vilken matris måste vara ortogonal?

Basbytesmatrisen. I denna uppgift: första rad (1,-1), andra rad (1,1).

Du behöver dela med rotenur(2) för att den ska bli ortogonal och det görs aldrig i facit.

Sambandet A^T = A^-1 gäller ju bara då.. 

Se vad jag skrev i den andra tråden. Repeterat nedan.

Jo, jag läste den tråden men håller inte med att den formeln stämmer såvida inte matrisen är ortogonal.

Nu ska jag sova. Får kolla litteraturen imorgon. Sov gott. 

Godmorgon. 

Jag vidhåller att det jag säger stämmer.

Patenterameras samband gäller endast då egenvektorerna är ortogonala och har längden 1 (normerade) , vilket de inte har i uppgiften. 

jamolettin skrev:

Godmorgon. 

Jag vidhåller att det jag säger stämmer.

Patenterameras samband gäller endast då egenvektorerna är ortogonala och har längden 1 (normerade) , vilket de inte har i uppgiften. 

Ja exakt det var därför jag ställde frågan, eftersom jag tänkte som du. Dock känns det samtidigt väldigt osannolikt att lärarna hade haft kvar facit om det var fel, så jag är i ett dilemma. 

Vi har att den kvadratiska formen Q kan uttryckas mha matriser i olika baser enligt

$Q\left(\overrightarrow{x}\right)={\left[\overrightarrow{x}\right]}_B^T{\left[Q\right]}_B{\left[\overrightarrow{x}\right]}_B={\left[\overrightarrow{x}\right]}_E^T{\left[Q\right]}_E{\left[\overrightarrow{x}\right]}_E$. E betecknar här standardbasen.

Vi kan nu utnyttja basbytesmatris.

${\left[\overrightarrow{x}\right]}_E=P_{B\to E}{\left[\overrightarrow{x}\right]}_B$.

Vi får då att 

${\left[\overrightarrow{x}\right]}_B^T{\left[Q\right]}_B{\left[\overrightarrow{x}\right]}_B={\left(P_{B\to E}{\left[\overrightarrow{x}\right]}_B\right)}^T{\left[Q\right]}_E{P}_{B\to E}{\left[\overrightarrow{x}\right]}_B={\left[\overrightarrow{x}\right]}_B^T{P}_{B\to E}^T{\left[Q\right]}_E{P}_{B\to E}{\left[\overrightarrow{x}\right]}_B$.

Eftersom detta skall gälla för alla $\overrightarrow{x}$ (och då vi begränsar oss till symmetriska matriser) så måste vi ha att

${\left[Q\right]}_B= P_{B\to E}^T{\left[Q\right]}_E{P}_{B\to E}$.

QED

Det gäller om P är en ortogonal matris. 

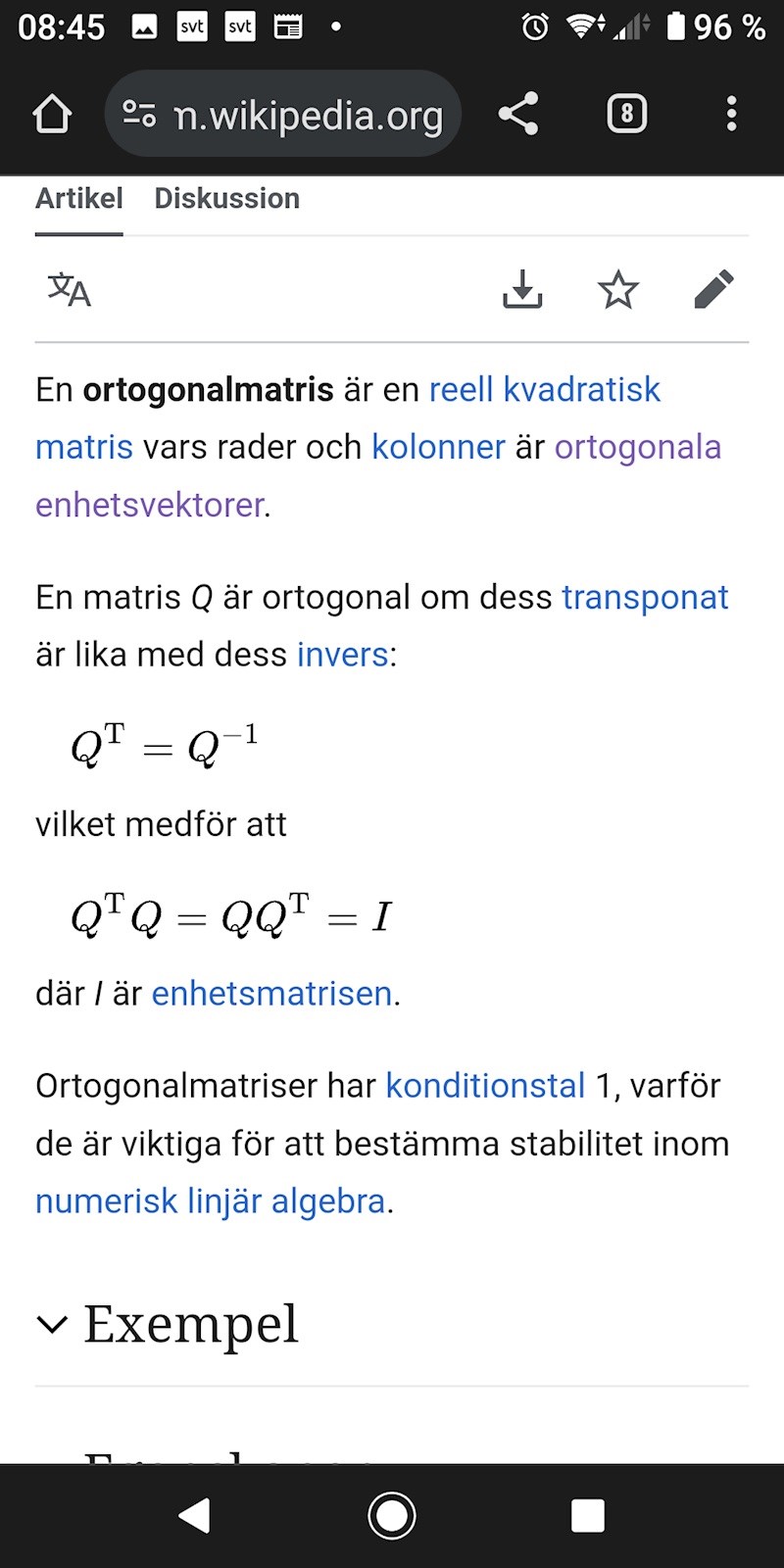
På vilket sätt berör detta hur man tar fram matrisen till en kvadratisk form i olika baser?

Det finns igen formel för hur matriserna för Q i olika baser relateras till varandra baserat på basbytesmatriserna mellan baserna.