Alla förutom en lösning fungerar i min trigonometriska ekvation

Jag har jobbat ett tag nu på denna uppgiften och hittat svaren men en av svaren går inte att sätta in i ursprungsekvationen och jag vet inte varför.

"Räkna i radianer. Lös fullständigt och exakt ekvationen: tan(2x+4)=tan(5x-1)"

$J a g h a r r ä k n a t s o m f ö l j a n d e : \tan (2 x + 4) = \tan (5 x - 1) \Leftrightarrow \frac{\sin (2 x + 4)}{\cos (2 x + 4)} = \frac{\sin (5 x - 1)}{\cos (5 x - 1)} \Leftrightarrow \sin (2 x + 4) = \frac{\sin (5 x - 1) \cdot \cos (2 x + 4)}{\cos (5 x - 1)} \Leftrightarrow \sin (2 x + 4) \cdot \cos (5 x - 1) = \sin (5 x - 1) \cdot \cos (2 x + 4) ⟺ \sin (2 x + 4) \cdot \cos (5 x - 1) - \sin (5 x - 1) \cdot \cos (2 x + 4) = 0 \Leftrightarrow J a g s e r a t t e k v a t i o n k a n s k r i v a s s o m a d d i t i o n s f o r m e l / s u b t r a k t i o n s f o r m e l \sin (x - y) : S u b s t i t u t i o n : (2 x + 4) = x (5 x - 1) = y A d d i t i o n s f o r m e l : \sin (x) \cdot \cos (y) - \cos (x) \cdot \sin (y) = \sin (x - y) ⟹ \sin (2 x + 4) \cdot \cos (5 x - 1) - \cos (2 x + 4) \cdot \sin (5 x - 1) = \sin ((2 x + 4) - (5 x - 1)) ⟺ \sin ((2 x + 4) - (5 x - 1)) = 0 ⟺ \sin (5 - 3 x) = 0 ⟺ N u b ö r j a r d e t " s v å r a " : 5 - 3 x = a r c \sin (0) + n \cdot 2 π & 5 - 3 x = π - a r c \sin (0) + n \cdot 2 π, n \in ℤ * < - D e n n a r a d v ä l j s s o m s t a r t f ö r m i t t a l t e r n a t i v a s v a r . - 3 x = 0 - 5 + n \cdot 2 π & - 3 x = (π - 0) - 5 + n \cdot 2 π x = \frac{0 - 5}{- 3} + \frac{n \cdot 2 π}{- 3} & x = \frac{(π - 0) - 5}{- 3} - \frac{n \cdot 2 π}{- 3} x_{1} = \frac{5}{3} - n \cdot \frac{2 π}{3} & x_{2} = \frac{π - 5}{3} - n \cdot \frac{2 π}{3} x_{1} f u n g e r a r i u r s p r u n g s e k v a t i o n e n m e n i n t e x_{2} s o m s v a r .$

$O v a n s e r n i e n h e t s c i r k e \ln m e d r a d i a n e r v i d 90, 180, 270 o c h 360 g r a d e r s m a r k e r i n g a r n a . (S o m h j ä l p f ö r a t t v i s u a l i s e r a a l l t) A l t e r n a t i v t h i t t a d e j a g o c k s å d e t t a s v a r (v i l k e t s o m o c k s å f u n g e r a r i u r s p r u n g s e k v a t i o n e n) : 5 - 3 x = a r c \sin (0) + n \cdot 2 π & 5 - 3 x = π - a r c \sin (0) + n \cdot 2 π, n \in ℤ * (B å d a e k v a t i o n e r o v a n g å r a t t k o m b i n e r a t i l l e n e n d a f u n k t i o n) 5 - 3 x = n \cdot π - 3 x = - 5 + n \cdot π x = - \frac{5}{- 3} + \frac{n \cdot π}{- 3} x_{3} = \frac{5}{3} - \frac{n \cdot π}{3}$

Hoppas någon ser vart det blev knas.. för jag ser inte det :/

Lösningen blir enklare utan sin och cos.

tan(u) = tan(v)

så är

v = u + nπ

Dr. G skrev:
Lösningen blir enklare utan sin och cos.
Om
tan(u) = tan(v)
så är
v = u + nπ

Aa okej det ser ju såklart väldigt mycket enklare ut men jag får inte använda något som jag själv inte kan härleda så varför stämmer detta samband du beskrev? Alternativt, vart kan jag läsa på om denna/vad heter det sambandet? :)

Jag har använt att

tan(u)

har period π och att den inom en period bara antar varje värde en gång.

Se enhetscirkeln varför tan-värdet upprepas efter ett halvt varv ( $\pi$ radianer):

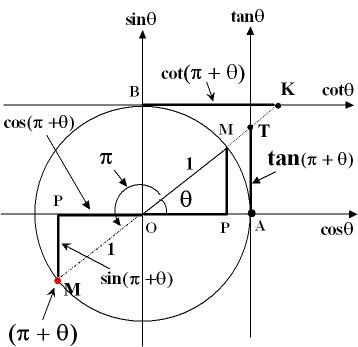
Det som är riskabelt med din metod är att du måste säkerställa att de ursprungliga nämnarna inte är lika med noll, d.v.s. att lösningarna uppfyller:

$\cos(2x+4)\ne 0$ och $\cos(5x-1)\ne 0$

Dr. G skrev:
Jag har använt att
tan(u)
har period π och att den inom en period bara antar varje värde en gång.

Okej är detta rätt då?

$\tan (2 x + 4) = \tan (5 x - 1) \Leftrightarrow 4 = 3 x - 1 \Leftrightarrow 3 x = 5 \Leftrightarrow x = \frac{5}{3}$

Är x bara 5/3? Är detta det fullständiga och exakta svaret på uppgiften? :O

Hur tänker jag med perioden man vanligtvis lägger till när man gör en invers?

För instinktiv vill jag egentligen göra såhär:

$\tan (2 x + 4) = \tan (5 x - 1) \Leftrightarrow 2 x + 4 + n π = 5 x - 1 + nπ \Leftrightarrow 4 + nπ = 3 x - 1 + nπ \Leftrightarrow nπ = 3 x - 5 + nπ \Leftrightarrow Men hur fortsätter jag ifall man gör såhär ?$

HarveySpecter skrev:
Dr. G skrev:
Jag har använt att
tan(u)
har period π och att den inom en period bara antar varje värde en gång.
Okej är detta rätt då?
$\tan (2 x + 4) = \tan (5 x - 1) \Leftrightarrow 4 = 3 x - 1 \Leftrightarrow 3 x = 5 \Leftrightarrow x = \frac{5}{3}$
Är x bara 5/3? Är detta det fullständiga och exakta svaret på uppgiften? :O
Hur tänker jag med perioden man vanligtvis lägger till när man gör en invers?
För instinktiv vill jag egentligen göra såhär:

$\tan (2 x + 4) = \tan (5 x - 1) \Leftrightarrow 2 x + 4 + n π = 5 x - 1 + nπ \Leftrightarrow 4 + nπ = 3 x - 1 + nπ \Leftrightarrow nπ = 3 x - 5 + nπ \Leftrightarrow Men hur fortsätter jag ifall man gör såhär ?$

Lägg till n*pi endast på ena sidan, som Dr. G skrev i första svaret.

Svara Avbryt

Visa senaste svar