Analys: trigfunktioner och godtyckligt liten period
Finns nån funktion som oscillerar lika frenetiskt som sin(1/x) gör i närheten av noll fast för alla x?
(Så att om jag plottar den så ser det ut som en solid rektangel oavsett hur mycket jag zoomar)
EDIT: Ja jag kom precis på att sin(1/x) ju inte ens är en periodisk funktion, så det finns ingen period. Men ni kanske förstår ändå
Tycker funktionen verkar täcka det mesta av skärmen.
Jag vet inte exakt vad du menar med "lika frenetiskt" men jag antar att du eftersöker en funktion med mycket hög frekvens för alla x. Du skulle väl kunna definiera en funktion:
Denna funktion är dock svår att plotta men du kan stoppa in valfritt litet tal istället för och få en rektangel:
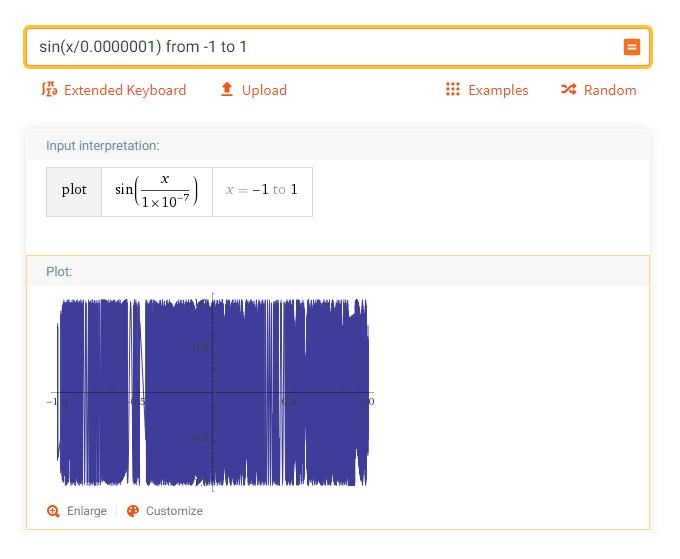
Truppeduppe: nääää hur ser den ut för dig?
Ebola: åh varför tänkte jag inte på det? Genialtiskt! Den beter sig ju som sin(1/x) kring noll, men för alla x.
Fast, vi får väl knappast någon väldefinierad funktion genom att sätta ?
Vad blir exempelvis ?
Men visst, jag tycker Ebola ändå är något kul på spåret. Kanske skulle idén kunna omformuleras till att visa att det finns - om inte oändligt frenetiska funktioner - så i vart fall godtyckligt frenetiska funktioner. Det finns säkert massa sätt att formalisera detta på, men ett spontant försök är följande:
För varje och varje existerar det en slät funktion , sådan att gör minst stycken teckenbyten på varje intervall av längd .
Bevis: Välj ett tillräckligt stort och sätt .
Limx->0sin(1/x) är väl inte definierat? Då ska denna funktion inte heller vara definierad nånstans eller?
Det enda jag ville ha var en ifylld rektangel egentligen, och det blir det ju. Den kanske inte är definierad någonstans pga samma anledning
Något som jag tycker talar emot att Qetsiyahs önskan om en 'oändligt frenetisk' funktion skulle gå att uppfylla är att exemplet egentligen inte är oändligt frenetisk någonstans i sin definitionsmängd. Ta vilket som helst, och zooma in tillräckligt långt, så ser vi att funktionen lokalt beter sig ganska lugnt och städat, ungefär som en vanlig sinusfunktion med en, visserligen väldigt hög, men ändock ändlig period.
Punkten där det intressanta oändligt urspråde beteendet tycks uppstå (och ständigt finnas kvar, hur mycket man än zoomar in!) är lite av en "skenpunkt". Den är ju faktiskt inte med i definitionsmängden! Därmed tror jag det blir svårt att hitta en funktion som immiterar just det här beteendet överallt, och samtidigt har punkter där den på riktigt är definierad.
Du får svårt att fylla en kvadrat med någon sinuskurva. Däremot finns det kurvor (dock inte funktionsgrafer) som kan fylla en kvadrat:
https://sv.wikipedia.org/wiki/Peanos_kurva
Att detta fungerar grundar sig i det ganska underliga faktumet att det i någon mån finns lika många punkter i en rektangel som på en linje.
oggih skrev:Egentligen inte är oändligt frenetisk någonstans i sin definitionsmängd.
Finns någon funktion som är det?
Punkten där det intressanta oändligt urspråde beteendet tycks uppstå (och finnas kvar, hur mycket man än zoomar in!) är lite av en "skenpunkt". Den är ju faktiskt inte med i definitionsmängden! Därmed tror jag det blir svårt att hitta en funktion som immiterar just det här beteendet överallt, och samtidigt har punkter där den på riktigt är definierad.
Det låter rimligt, så kanske det är (tyvärr för mig, men hurra för min mobil och wolframalpha).
Som Alvin gett exempel på så finns ju däremot kurvor som är "space filling". Nu börjar jag tänka på måtteori.
Det finns många olika sätt som en funktion kan vara extremt frenetisk på.
Om vi ger upp släthet så skulle vi kunna titta på Weirstrassfunktionen som "aldrig någonsin vilar", och som har en så pass "taggig" graf att det inte finns en enda punkt där den är deriverbar, trots att den är kontinuerlig överallt.
Om det var teckenförändringar vi ville ha, och är beredda att ge upp kontinuitet, så kan vi dra till med något så monstruöst som
som gör oändligt många teckenbyten i varje öppet intervall. Det känns också som ett ganska frenetiskt beteende! :D
Oändligt frenetiska funktioner är inte alls bara en lek med fantasin! (Verkar det som). Jag läste om Riemann-Lebesgue-lemmat, titta:
 Det är frenetiken som gör att integralens värde blir noll; funktionen f:s beteende spelar ingen roll.
Det är frenetiken som gör att integralens värde blir noll; funktionen f:s beteende spelar ingen roll.
Wow! Har aldrig tänkt på att det skulle vara en konsekvens av "frenetiskhet", men nu när du säger det makear det ju faktiskt väldigt mycket sense (i alla fall om är kontinuerlig).
Hur ser resten av beviset ut? Vad används lemmat till i boken du läser?
Kan du inte gissa det? Konvergens, integraler, en sinusfunktion multiplicerad med en godtycklig funktion... Fourieranalys!
Lemmat är jätteviktig i boken.
Visa spoiler


fff
Är konvergensen av fresnelintegralen (noll till oändlighet av sin(x^2)) ett resultat av frenetiskhet?
Skillnaden mellan den och sin(x) (som ju inte är konvergent, men som man skulle kunna tro är lika med noll) är att perioden blir godtyckligt liten i oändligheten.
Hur snabbt måste perioden minska för att integralen ska vara konvergent? Alltså, hur snabbt ska f i sin(f(x)) öka? Jag vet inte hur jag ska googla det här på engelska.
(Jag vet att funktionen inte ens är periodisk men ni förstår ändå)
Vad är speciellt med den funktionen?
Jag såg att du redigerade ditt inlägg men varflr? Funktionen är definierad för negativa x (även hela negativa x)
där och är en uppräkning av de positiva rationella talen.
Ta litet eget initiativ och analysera funktionen på egen hand, istället för att vänta på att någon ska ställa en fråga om den. Ställ några egna frågor om dess egenskaper och besvara dem.
Exempelvis, är funktionen överhuvudtaget definierad? i så fall, vad är dess definitionsmängd och värdemängd?
Det första jag gjorde var att plotta den, men jag såg ingen likhet med sin(x^2), eller varför den är relevant i frågan.
Exempelvis, är funktionen överhuvudtaget definierad? i så fall, vad är dess definitionsmängd och värdemängd?
Ja det också
Konceptet om oändlig frekvens kom upp i reglerteknikkursen jag går nu. För de flesta system gäller att en tillräckligt snabbt oscillerande sinus insignal ger ingenting som utsignal.
Min lärare använde analogin om en svängande bilratt; om den svänger väldgit snabbt åker bilen in fact rakt.
Matematiskt innebär det för en differentialekvation med en tvingande funktion att dess överföringsfunktion (funktionen som fås vid laplacetransform och omskrivning dvs ) har egenskapen att .





