Analysens huvudsats och funktionens deriverbarhet
Hej, jag har en fråga angående analysens huvudsats som jag har bifogat nedan:

Min fråga är varför det räcker med att funktionen f ska vara kontinuerlig för att funktionen S ska vara deriverbar, vi vet ju att deriverbarhet medför kontinuitet men inte omvänt, se figur nedan:
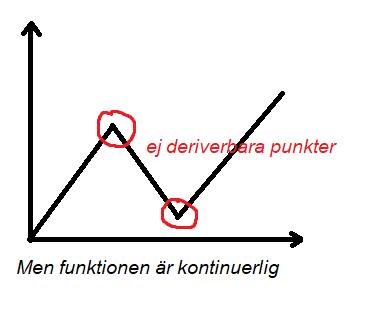
Det verkar vara något jag missar här?
Tack för all hjälp i förhand!
Det är väl en av sakerna som satsen säger. Då är deriverbar med derivatan Enligt definition måste vi visa att gränsvärdet
existerar. Då är ju deriverbar. Jag antar att de visar detta i din boks bevis, men om jag minns rätt är huvudsteget medelvärdessatsen för integraler. Vi har väl
Medelvärdessatsen för integraler hjälper oss nu se att gränsvärdet verkligen är lika med och därmed existerar gränsvärdet. För att se det sistnämnda krävs det att funktionen är kontinuerlig på (en förutsättning för medelvärdessatsen bland annat), men inget mer.
Happyeagle skrev:Det är väl en av sakerna som satsen säger. Då är deriverbar med derivatan Enligt definition måste vi visa att gränsvärdet
existerar. Då är ju deriverbar. Jag antar att de visar detta i din boks bevis, men om jag minns rätt är huvudsteget medelvärdessatsen för integraler. Vi har väl
Medelvärdessatsen för integraler hjälper oss nu se att gränsvärdet verkligen är lika med och därmed existerar gränsvärdet. För att se det sistnämnda krävs det att funktionen är kontinuerlig på (en förutsättning för medelvärdessatsen bland annat), men inget mer.
Alright, jag köper ditt resonemang, men hur behandlar satsen punkter på f(x) som inte är deriverbara, men kontinuerliga?
Satsen säger att f är en derivata. f behöver inte själv kunna deriveras för att vara en derivata till en annan funktion.
Tänk att du delar upp din kantiga kurva i hörnen så du får tre linjestycken. Linjer integreras till andragradskurvor, eller hur? Så S(x) kommer se ut som hoplimmade bitar från tre olika andragradskurvor. Att f är kontinuerlig överallt innebär att lutningen på S-kurvan ändras utan plötsliga hopp - dvs, S kommer inte få den sortens kanter som f har.
Skaft skrev:Satsen säger att f är en derivata. f behöver inte själv kunna deriveras för att vara en derivata till en annan funktion.
Exakt det jag tänkte säga, det gäller att läsa noga vad påsåendet påstår!
Skaft skrev:Satsen säger att f är en derivata. f behöver inte själv kunna deriveras för att vara en derivata till en annan funktion.
Tänk att du delar upp din kantiga kurva i hörnen så du får tre linjestycken. Linjer integreras till andragradskurvor, eller hur? Så S(x) kommer se ut som hoplimmade bitar från tre olika andragradskurvor. Att f är kontinuerlig överallt innebär att lutningen på S-kurvan ändras utan plötsliga hopp - dvs, S kommer inte få den sortens kanter som f har.
Okej, jag har en följdfråga på ditt andra stycke, jag ställde upp följande funktion: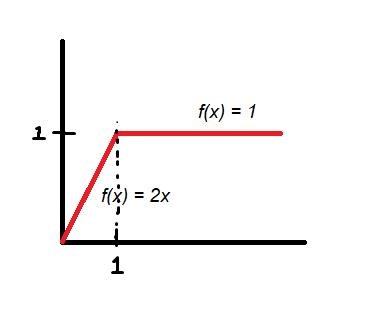
Och tar integralen av den, (den bör vara riemann integrerbar om jag inte misstar mig), vi får att integralen blir från 0 till x: x^2 för [0,1] och 1 + ( x - 1 ) för ]0,oändlighet[, här får jag två olika derivator vid punkten x=1 om jag kommer från höger eller vänster, detta betyder ju att den inte är deriverbar vid x=1 (enligt derivatans definition?). Hur går detta ihop med att satsen säger att funktionen S (som i vårt fall var x^2 för [0,1] och 1 + ( x - 1 ) för ]0,oändlighet[) är deriverbar, när den i x=1 inte är deriverbar?
y=2x går inte genom punkten (1, 1), så exemplet haltar lite. Men det låter fortfarande som att du blandar ihop f och S. S är deriverbar, f är det inte (i dina exempel). Hur ser S-kurvan ut, om du skissar den?
Som skaft säger går inte y=2x genom punkten (1,1). Däremot gör ju y=x det. Arean blir x^2/2 för x i [0,1]. Arean för x större än 1 blir 1/2+(x-1). (Triangeln med bas 1 och höjd 1 har area en halv). Om vi deriverar uttrycken och sätter in x=1 får vi samma svar(1).
Skaft skrev:y=2x går inte genom punkten (1, 1), så exemplet haltar lite. Men det låter fortfarande som att du blandar ihop f och S. S är deriverbar, f är det inte (i dina exempel). Hur ser S-kurvan ut, om du skissar den?
Nu pratar jag bara om S' i satsen (vilket i mitt exempel är benämnt f(x)) alltså det du pratade om i ditt andra stycke i ditt första svar. Jag skulle fortfarande säga att funktionen S' (som jag benämnde f(x) i figuren) är odefinenierad i x = 1 eftersom höger och vänster derivatorna inte stämmer överens:
då . Om man använder derivations reglerna på min funktion f(x), så som ni verkar ha gjort, så är det förutsatt att höger och vänster derivatorna är lika varann vilket i vårt fall det inte är.
Hur kan satsen säga att S är deriverbar? Det jag hellre skulle vilja säga är att S är styckvis deriverbar?
S'(1) = 1.
Är du med på att din graf borde se ut så här?

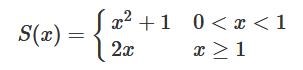
Högerderivatan och vänsterderivatan i punkten antar samma värde, .
S är deriverbar. f är kontinuerlig.
Edit: Saknades en konstantterm i uttrycket
HaCurry skrev:Jag skulle fortfarande säga att funktionen S' (som jag benämnde f(x) i figuren) är odefinenierad i x = 1
Nejdå, f(1) är inte odefinierat. f behöver inte vara deriverbar för att ha ett värde i x=1. f(1) kan antingen läsas av i grafen eller räknas ut genom att sätta in x=1 i ekvationen (dessa stämmer dock inte överens men det är ett sidospår).
Om man använder derivations reglerna på min funktion f(x), så som ni verkar ha gjort, så är det förutsatt att höger och vänster derivatorna är lika varann vilket i vårt fall det inte är.
Nej, f(x) ska som sagt inte deriveras. f(x) är en derivata, inte något som deriveras. S(x) är deriverbar, därför att dess derivata f(x) är kontinuerlig. Derivatan behöver inte vara deriverbar. Se (slarvigt ritat) exempel. Röd är derivatan f, blå är integralen S. Först växer den som en andragradskurva, sen går den över till att växa linjärt. Notera att blå kurva är helt kantfri, trots att dess derivata har en kant. Det beror på att f är kontinuerlig.
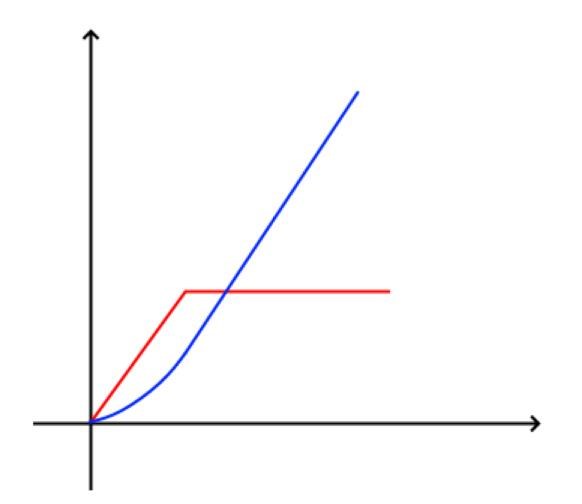
Ber om ursäkt alla, jag har förvirrat mig själv och förvirrat er, verkar som att jag blandar ihop notationen, jag ska läsa igenom era svar och så får jag återkomma med tydligare frågor, (sånt som händer när man gör matte 3 på natten).
Haha ingen fara, men är detta verkligen matte3?
Det skulle nog läsas som "matte kl 3 på natten", inte kurs 3 :)
Åh... man bör inte skriva på pluggakuten på natten heller hahaha






