Ange cotangens i ett visst intervall?
Om sinα = 1/7, och π/2 < α < π så gäller att cotα är lika med
(a)− 1/4√3; (b)−4√3; (c)± 1/(4√3); (d)annatsvar
SVAR b)
jag förstår att (a) är tangens och att (b) är cotangens nu när jag tittade på facit, jag förstår också att b) kan vara svaret ty sin är positiv så cos måste vara negativ på det angivna intervallet, därav kan svaret icke vara c). men hur ska jag veta vilken av a) och b) är rätt? man får heller inte använda miniräknare så jag undrar nu hur jag ska veta med säkerhet att det är just talet −4√3? Svaret kunde lika gärna varit d)?
Hur löser man det här?
Rita enhetscirkeln. Använd trigonometriska ettan för att beräkna cos. 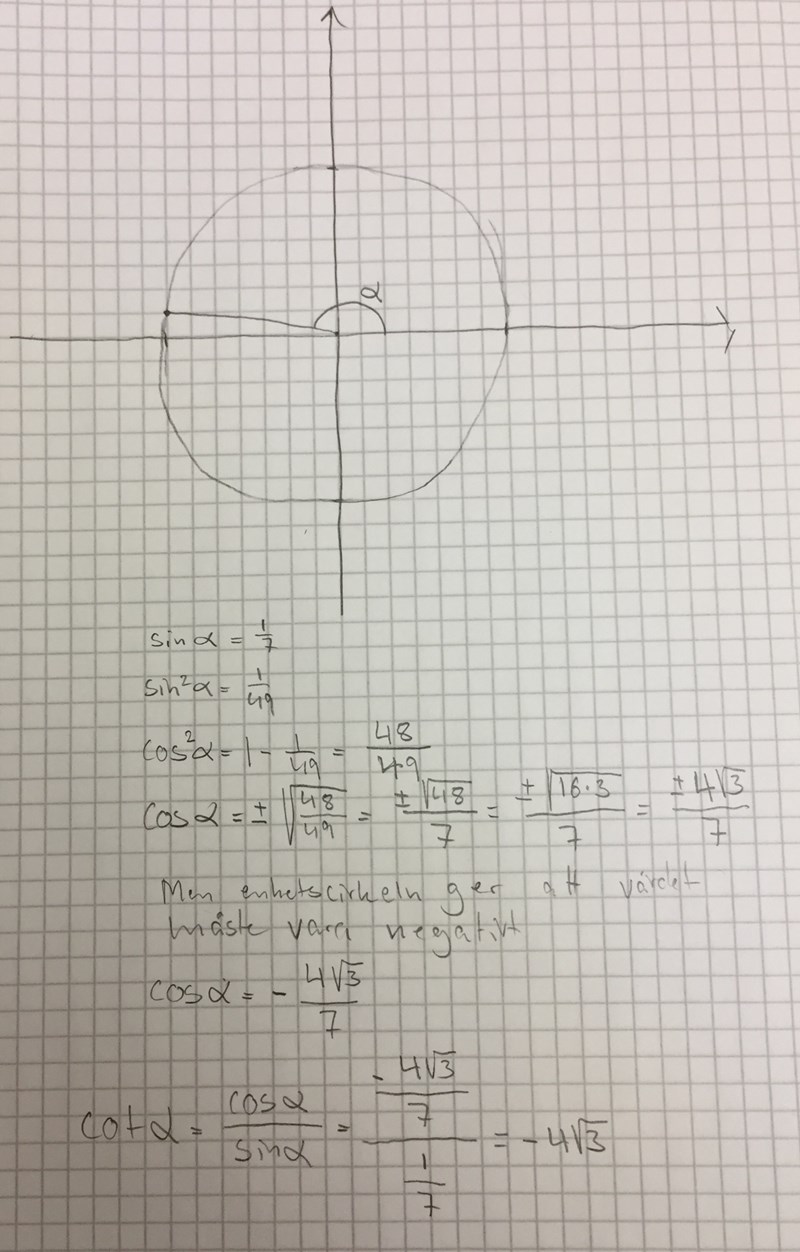
Man börjar med att rita upp enhetscirkeln och markerar på ett ungefär var vinkeln befinner sig. Eftersom du vet att sinα = 1/7 och att vi är i andra kvadranten kan vi få fram cosinus för vinkeln med hjälp av trigonometriska ettan och att vi vet att cosinus är negativt. Sedan behöver man bara titta på definitionen av cotangens för att räkna färdigt. Lite elak uppgift, tycker jag!


