Areaberäkning av ett område som begränsas av två stycken kurvor
Hej jag har fastnat med en uppgift.
Uppgiften lyder såhär: Beräkna arean av området som begränsas av kurvorna y = -x^2+6 och y = x^2-2x-6.
Jag skrev in båda kurvorna in i GeoGebra och fick grafen: 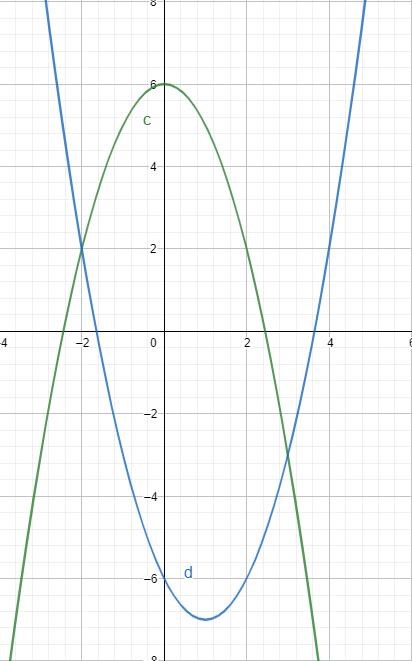
Jag vet inte riktigt vilka integrationsgränser jag ska använda, men resten för att lösa uppgiften tror jag att jag vet hur man gör.
Steg 1: A =((f(x)-g(x))dx
Steg 2: Integrera
Steg 3: Sätta in integrationsgränserna i formeln för F(a)-F(b)
Mvh Florian.
Välkommen till Pluggakuten!
Sätt de båda y-värdena lika med varandra och lös ekvationen.
Florian Koch skrev:Hej jag har fastnat med en uppgift.
Uppgiften lyder såhär: Beräkna arean av området som begränsas av kurvorna y = -x^2+6 och y = x^2-2x-6.
Jag skrev in båda kurvorna in i GeoGebra och fick grafen:
Jag vet inte riktigt vilka integrationsgränser jag ska använda, men resten för att lösa uppgiften tror jag att jag vet hur man gör.
Steg 1: A =((f(x)-g(x))dx
Steg 2: Integrera
Steg 3: Sätta in integrationsgränserna i formeln för F(a)-F(b)
Mvh Florian.
Det är viktigt att veta
- Vilket område i figuren som du ska areaberäkna. Detta bestämmer hur du får fram integrationsgränserna.
- Vilken funktion som är den "övre" och vilken som är den "undre" funktionen i figuren. Detta bestämmer vilken funktion som är f(x) och vilken som är g(x).



