Beräkna area av ytan mha dubbelintegral
Hej. Jag har en uppgift där jag ska beräkna
Jag tänkte att ytan är den sneda cirkeln som skapas då ytan skär cylindern. Därför försökte jag hitta gränserna för radien.

Men i facit så räknar dom såhär: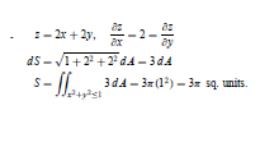
Ja, de procjicerar den sneda ytan på enhetscirkeln (cylinderns bottenarea). Är nog det smidigaste sättet att lösa denna uppgift. Läs mer här:
http://ingforum.haninge.kth.se/armin/ALLA_KURSER/SF1626/YTINTEGRALER.pdf
Jag förstår inte. Varför skulle radien variera från till ? Områdets projektion i -planet är ju cirkeln . I detta område varierar radien mellan och . Då får du samma svar som facit.
jaha så formeln
så är D projectionen på xy planet då två plan skär sig? Gäller det här endast för beräkning av då jag ska beräkna area av funktionsyta?
Du börjar ju med ytintegralen:
där är den tredimensionella ytan vi söker arean på. För att kunna integrera lättare vill vi då integrera i -planet. Genom att utnyttja att kan vi istället integrera över projektionen av området i -planet:
Notera att egentligen är en specialfall då ytan är given på explicit form () av en mer generell formel, nämligen:
(En intuition för varför detta gäller är att absolutbeloppet av kryssprodukten ger arean av parallellogrammen som vektorerna spänner upp. Absolutbeloppet av kryssprodukten mellan derivatorna ger då arean på ett litet parallellogram som approximerar ytan. När vi sedan integrerar blir parallellogrammen mindre och mindre, och approximationen går mot det exakta värdet. Vi multiplicerar alltså funktionens värde [i detta fall ] med arean av ett litet parallellogram på ytan och integrerar.)
Om vi har en yta på explicit form är en enkel parametrisering . Derivatornas kryssprodukt blir då:
Absolutbeloppet av detta ger sedan det välbekanta uttrycket från tidigare:



