Beräkna integral

Den här frågan printar jag ut och skickar till mig själv 10 år fram i tiden. Han kanske kan.

Nej men ärligt talat är det enda jag lärt mig partialbråksuppdelning, variabelsubs och partiell integration. Dessa tar mig ingenstans

Qetsiyah skrev:

Den här frågan printar jag ut och skickar till mig själv 10 år fram i tiden. Han kanske kan.

Nej men ärligt talat är det enda jag lärt mig partialbråksuppdelning, variabelsubs och partiell integration. Dessa tar mig ingenstans

Om du kan dessa tre metoder skulle jag säga att du kan lösa a)-uppgiften redan idag. Det är nämligen inget särskilt avancerat som krävs, man måste bara tillämpa metoderna på ett väldigt finurligt sätt. Jag skulle tippa på att du kommer förstå lösningen till a)-uppgiften när du ser den, men antagligen kommer tänka "hur fan kom någon på det här?". :-)

(b)-uppgiften kanske dock ska vänta till en framtida version med lite mer universitetsmatte under bältet.)

Då ska jag försöka.

Vad för universitetsmatte?

Löste a) enligt nedan:

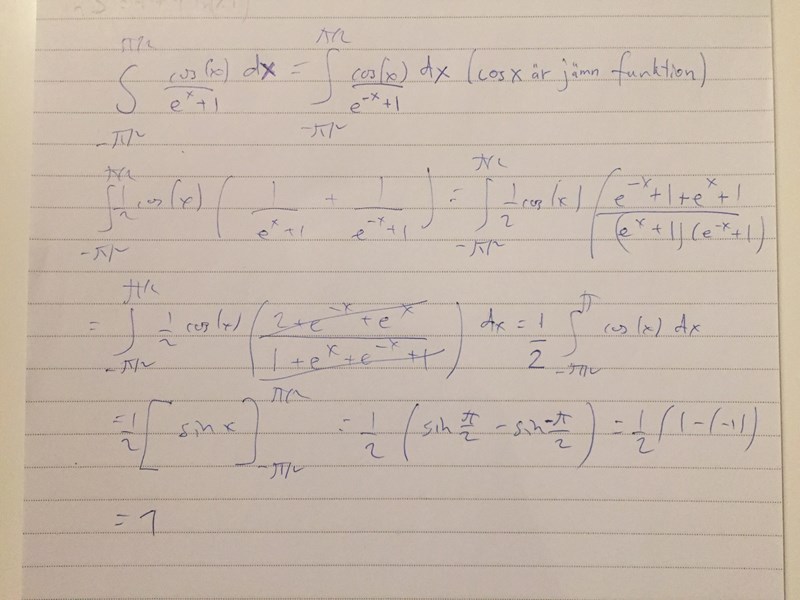
tomast80 skrev:

Löste a) enligt nedan:

Visa spoiler

Så elegant! Får verkligen hålla med omvad AlvinB skrev:

Jag skulle tippa på att du kommer förstå lösningen till a)-uppgiften när du ser den, men antagligen kommer tänka "hur fan kom någon på det här?". :-)

Kan du förklara hur du kom på det? Det är verkligen att krångla till något för att kunna förenkla det sedan!

Tackar!

Insåg att täljaren är en jämn funktion och sen är det ett symmetriskt intervall. Det innebär att om man byter ut $x$ mot $-x$ i integralen måste det bli samma värde på hela integralen, d.v.s.:

$\displaystyle \int_{-\pi/2}^{\pi/2}\frac{\cos x}{e^x+1}dx=$

$\displaystyle \int_{-\pi/2}^{\pi/2}\frac{\cos (-x)}{e^{-x}+1}dx=$

{$\cos (-x)=\cos x$}

$\displaystyle \int_{-\pi/2}^{\pi/2} \frac{\cos x}{e^{-x}+1}dx$

Därmed kunde jag ta hälften av de två integralerna och lägga ihop och hoppades att delarna med ”e” skulle försvinna, vilket de mycket riktigt gjorde. Det var på ren intuition.

tomast80 skrev:

Löste a) enligt nedan:

Visa spoiler

Snyggt, tomast!

Som du konstaterat ger substitutionen $t=-x$ att:

$I=\displaystyle\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{\cos(x)}{e^x+1}\ dx=-\int_{\frac{\pi}{2}}^{-\frac{\pi}{2}}\frac{\cos(-t)}{e^{-t}+1}\ dt=\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{\cos(t)}{e^{-t}+1}\ dt$

Om vi sedan adderar ihop de två varianterna av integralen får vi en mycket trevlig förenkling:

$\displaystyle I+I=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{\cos(x)}{e^x+1}+\frac{\cos(x)}{e^{-x}+1}\ dx=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{\cos(x)}{e^x+1}+\frac{\cos(x)}{e^{-x}(1+e^x)}\ dx$

$I=\displaystyle\frac{1}{2}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{\cos(x)}{e^x+1}+\frac{e^x\cos\left(x\right)}{1+e^x}\ dx=\frac{1}{2}\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{\cos\left(x\right)(1+e^x)}{e^x+1}\ dx=\frac{1}{2}\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\cos\left(x\right)\ dx$

Man kan då börja undra vad som gjorde denna förenkling möjlig. Det är nämligen att $\cos(x)$ är en jämn funktion. Vi kan på samma sätt härleda att följande gäller för alla jämna funktioner $f(x)$:

$\displaystyle\int_{-a}^a\frac{f(x)}{e^x+1}\ dx=\frac{1}{2}\int_{-a}^a f\left(x\right)\ dx=\int_0^a f\left(x\right)\ dx$

Detta ger oss även en start på b)-uppgiften, eftersom även dess täljare är jämn. Dock är den resulterande integralen inte lika enkel; den kräver ett par kluriga knep och ganska goda kunskaper om serier och taylorutveckling.

Men vad är det då som gör den där nämnaren, $e^x+1$, så speciell? Finns det kanske fler nämnare som ger samma effekt?

Svaret är ja. Om vi söker funktioner $g(x)$ sådana att:

$\dfrac{f(x)}{g(x)+1}+\dfrac{f(x)}{g(-x)+1}=f\left(x\right)$

finner vi efter lite algebra att villkoret

$g\left(-x\right)=\dfrac{1}{g(x)}$

måste gälla på funktionen $g(x)$. Vi ser tydligt att $g(x)=e^x$ uppfyller detta eftersom $e^{-x}=1/e^x$. Men vi kan även notera att funktioner på formen $g(x)=e^{h(x)}$ där $h(x)$ är en udda funktion eftersom det då gäller att $e^{h(-x)}=e^{-h(x)}=1/e^{h(x)}$. Vi kan till exempel ta $h(x)=\sin(x)$ och inse att värdena för integralerna:

$\displaystyle\int_{-\frac{\pi}{2}}^\frac{\pi}{2}\frac{\cos(x)}{e^{\sin(x)}+1}\ dx$

$\displaystyle\int_{-1}^1\frac{\ln(x^2)\ln(1-x^2)}{e^{\sin(x)}+1}\ dx$

är samma som i $a)$- respektive $b)$-uppgiften. (Den övre integralen går dock i det här fallet att beräkna med hjälp av substitution)

Men det är inte bara exponentialfunktioner som uppfyller detta villkor. Vi kan även exempelvis ta funktionen:

$g\left(x\right)=\dfrac{1-x}{1+x}$

som även den uppfyller vårt villkor:

$g\left(-x\right)=\dfrac{1+x}{1-x}=\dfrac{1}{\frac{1-x}{1+x}}$

Man kan även generalisera detta ytterligare och finna att alla funktioner på formen:

$g\left(x\right)=\dfrac{p(x)+q(x)}{p(x)-q(x)}$

där $p(x)$ är jämn och $q(x)$ är udda uppfyller funktionalvillkoret.

En annan fråga är då om det finns något motsvarande villkor för $g(x)$ om $f(x)$ är udda. Dessvärre har jag inte lyckats finna några lösningar till funktionalekvationen som då uppstår.

AlvinB, verkade inte vara någon som lyckades lösa b), så kanske lika bra att du presenterar din lösning?

Ja, mitt mål var att hitta en krånglig integral där integranden är en jämn funktion, men det kanske blev lite väl svårt. Hur som helst följer min lösning här: