Beräkna linkrafter
Hej, i denna uppgift skall jag beräkna linkrafterna av Sab och Sac,
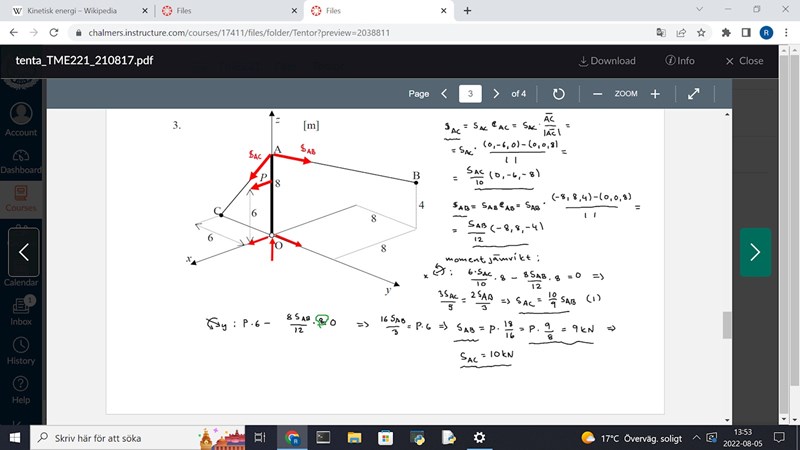
Det som jag undrar är varför man multiplicerar Sab med 8 två gånger när man beräknar dess moment runt y axeln (gröna inringade området)? Lite svårt att se men det skall se ut såhär:
Förstår att en av åttorna är ju avståndet från y axeln, dvs 8 enheter från y axeln längs med z axeln. Vart kommer den andra åttan ifrån?
Tack!
De har ju definierat x-komponenten av som
D4NIEL skrev:De har ju definierat x-komponenten av som
Hur vet man att det är x komponenten då som bildar momentet? Förstår inte hur ser man ser det?
Kan det vara så att om man exempelvis skall beräkna moment runt z axeln så multiplicerar man kraften med x och y komponenten alltid?
Vilket moment runt z-axeln ger en kraft som är riktad i z-led?
Bubo skrev:Vilket moment runt z-axeln ger en kraft som är riktad i z-led?
Det bör väl vara x och y axeln? Eller har jag helt fel?
Jag förstår inte riktigt vilken fråga du svarar på.
Vad blir momentet runt en flaggstång, av en kraft rakt uppåt?
mekatronik skrev:D4NIEL skrev:De har ju definierat x-komponenten av som
Hur vet man att det är x komponenten då som bildar momentet? Förstår inte hur ser man ser det?
Kan det vara så att om man exempelvis skall beräkna moment runt z axeln så multiplicerar man kraften med x och y komponenten alltid?
Om du har en kraft som angriper i punkten så ges momentet av
Vi kan plocka ut y-komponenten (dvs momentet kring y-axeln) med en enkel skalärprodukt
I ditt fall är och samt , alltså
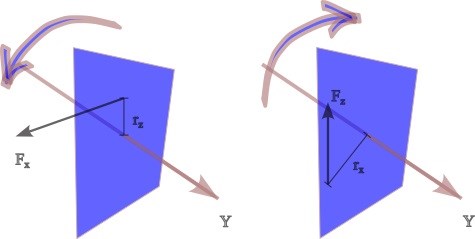
Jag tycker dock inte det är svårt att se hur krafterna i xz-planet vill rotera en godtycklig blå blubb runt y-axeln. Positiv rotation moturs sett från spetsen av y-axeln.
D4NIEL skrev:mekatronik skrev:D4NIEL skrev:De har ju definierat x-komponenten av som
Hur vet man att det är x komponenten då som bildar momentet? Förstår inte hur ser man ser det?
Kan det vara så att om man exempelvis skall beräkna moment runt z axeln så multiplicerar man kraften med x och y komponenten alltid?
Om du har en kraft som angriper i punkten så ges momentet av
Vi kan plocka ut y-komponenten (dvs momentet kring y-axeln) med en enkel skalärprodukt
I ditt fall är och samt , alltså
Jag tycker dock inte det är svårt att se hur krafterna i xz-planet vill rotera en godtycklig blå blubb runt y-axeln. Positiv rotation moturs sett från spetsen av y-axeln.
Tack för förklaringen, nu vet jag hur jag skall lösa dessa problem framöver.
Tack tack tack!!!!

