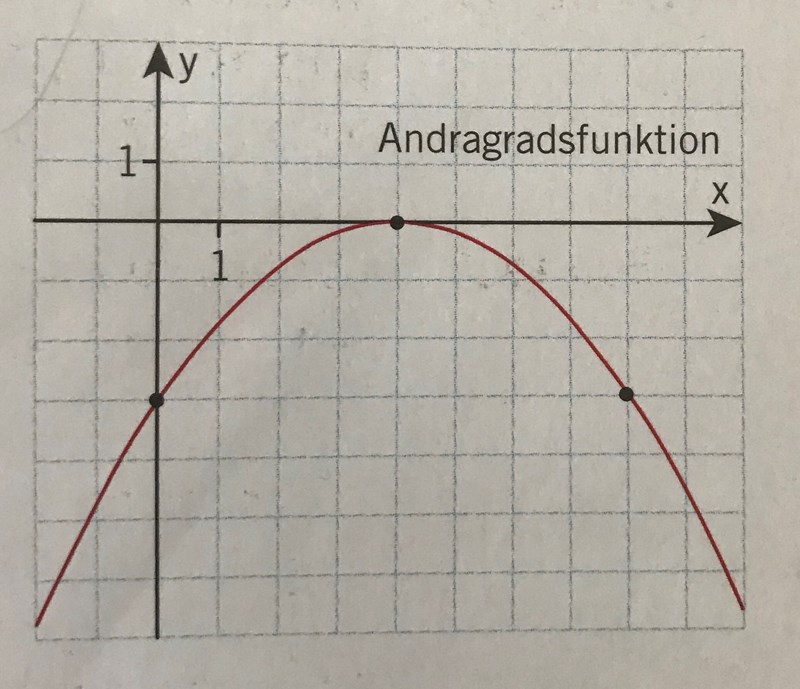
Bestäm en formel för y.
 Hej !
Hej !
Enligt andragradsekvation formeln Y=ax^2+bx+c.
C=-3
symmetrilinjen =4
kurvan är negativt:-ax.
resten behöver hjälp. Tack 🙏.
Får man fundera över derivatan i punkten (0, -3)?
Affe Jkpg skrev:Får man fundera över derivatan i punkten (0, -3)?
Jag studerar matte 2b , har inte derivatan.
Om man vet symmetrilinjen x = a så kan man alltid skriva funktionen som för något C, men det kanske man inte lär sig.
Annars kan du sätta in de tre punkter som du känner till, så får du ett ekvationssystem för a, b och c.
Två obekanta (a och b) och två ekvationer? :
Laguna skrev:Om man vet symmetrilinjen x = a så kan man alltid skriva funktionen som för något C, men det kanske man inte lär sig.
Annars kan du sätta in de tre punkter som du känner till, så får du ett ekvationssystem för a, b och c.
Hej Laguna!
Om jag skriv rätt borde talen vara i formeln som y = a16+b4-3.
men vidare kan jag inte.
Om jag skriv rätt borde talen vara i formeln som y = a16+b4-3.
Alla andragradskurvor kan beskrivas på många olika sött, t ex
y=ax2+bx+c
y=k(x-x1)(x-x2) där x1 och x2 är nollställen till funktionen
y=g(x-s)2+m där s är x-värdet för symmetrilinjen
och man kan skriva om en andragradskurva skriven på en form till en annan form.
I ditt fall tycker jag att det skulle vara enklast att beskriva den på det tredje sättet, men det är möjligt att facit beskriver den på det första sättet.
Laguna skrev:Om man vet symmetrilinjen x = a så kan man alltid skriva funktionen som för något C, men det kanske man inte lär sig.
Annars kan du sätta in de tre punkter som du känner till, så får du ett ekvationssystem för a, b och c.
Oj, det var ju fel. Men det stämmer när vertex har y = 0.
Smaragdalena skrev:Alla andragradskurvor kan beskrivas på många olika sött, t ex
y=ax2+bx+c
y=k(x-x1)(x-x2) där x1 och x2 är nollställen till funktionen
y=g(x-s)2+m där s är x-värdet för symmetrilinjen
och man kan skriva om en andragradskurva skriven på en form till en annan form.
I ditt fall tycker jag att det skulle vara enklast att beskriva den på det tredje sättet, men det är möjligt att facit beskriver den på det första sättet.
Jo, visst finns det nollställen: x=4 är en dubbelrot.
Affe Jkpg skrev:
Hej
tack för svaret. Det är faktiskt komplicerat för mig, jag förstår vissa del men inte helt.
Det som jag inte förstår y=(4)?? resten framför den jag vet.
y=(8)och resten framför den förstår inte.
det förstår jag men b vet inte.
Förstår att du inte förstår det står inte y=(4) Det står y(4). Det betyder vad är y när x = 4. Så du sätter in i din ekvation som du har olika x-värden och läser av i grafen vilket y värde det motsvarar.
Du väljer tre punkter som du ser i figuren och gör tre ekvationer med x och y som du sen kan se som ett ekvationssystem. Kombinera dem så får du ut a, b och c. Det är vad Affe har gjort. Så gör det själv så hoppas jag att det klarnar. 3 ekvationer och 3 obekanta a, b och c.
Det som jag inte förstår y=(4)?? resten framför den jag vet.
Mer korrekt notation är:
y = f(x) = ax2 + bx - 3
osv.
det förstår jag men b vet inte.






