Bestämma tredjegradspolynom utifrån graf
Hej!
Fastnar på denna uppgift.
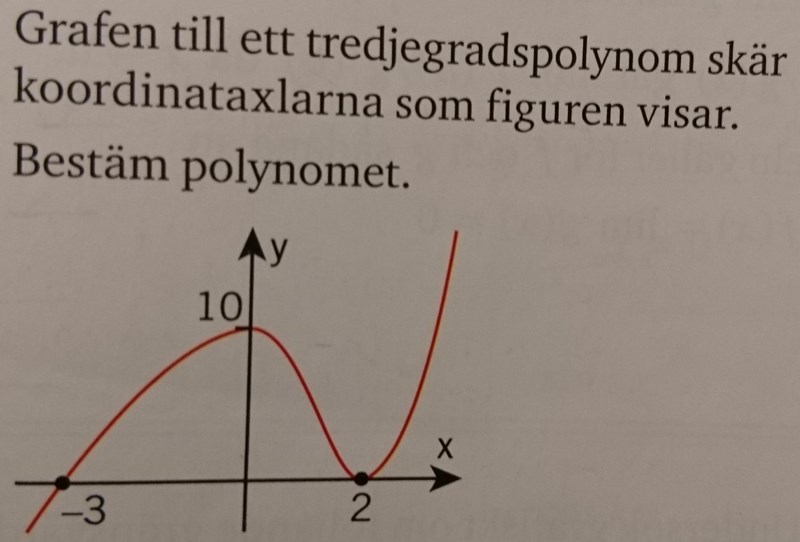
Min lösning: Tredjegradspolynom kan skrivas på formen p(x)=k(x-a)(x-b)(x-c). Vi har två nollställen i bilden (x=-3 resp. x=2) - egentligen tre, men vi ser inte vilket av nollställena som det är dubbelt av. Hade vi haft det sista nollstället kunde vi stoppa in koordinaten (0,10) och räkna ut k, men nu går det inte. Om vi däremot hittar ett samband till kan vi ställa upp ett ekvationssystem med två variabler. Är det det man ska göra i detta fall?
En bra sak att veta:
Titta på hur grafen ser ut vid rötterna. Vid så är den för växande och för fortfarande växande. Sedan i intervallet är funktionen avtagande och sedan för är den växande.
En rot upprepas alltid (har jag för mig?) om den vid roten ändrar från växande till avtagande, eller tvärtom. Du kan alltså direkt säga att är en dubbelrot.
Jaha! Det stämmer att 2 är dubbelrot, för facit anger detta, men inte hur de kom fram till det. Detta är helt ny information för mig, vad jag vet har det inte nämnts i vår undervisning/i läroböckerna. Men högst relevant att veta oavsett. Tack, då kan jag lösa uppgiften med min önskade metod!
Om man deriverar ett polynom med en dubbelrot så finns den faktorn kvar i derivatan, så dubbelroten är också en extrempunkt.
Faxxi skrev:Jaha! Det stämmer att 2 är dubbelrot, för facit anger detta, men inte hur de kom fram till det. Detta är helt ny information för mig, vad jag vet har det inte nämnts i vår undervisning/i läroböckerna. Men högst relevant att veta oavsett. Tack, då kan jag lösa uppgiften med min önskade metod!
En dubbelrot har formen .
På grund av tvåan i exponenten så är denna faktors värden symmetriska kring . Det betyder att polynomets värde inte byter tecken runt en dubbelrot.
Därav utseendet att grafen tangerar x-axeln vid nollstället och sedan vänder tillbaka igen.
Stort tack för era förklaringar!



