Blockmatriser
Jag vill bevisa att blockmatrisen [ A B har det(M)=det(A)det(D-CA-1B) om A-1 existerar och A samt B är kvadratiska.
C D]
Hur ska jag börja då?
Jag startade med att bevisa att det(A)det(D-CA-1B)=det(AD-CB) men det(AD-CB) gäller ju endast om AC=CA men det kan jag ju inte veta?
Om och är kvadratiska så måste och också vara kvadratiska. Säg att och har dimension och att och har dimension . Testa försöka skriva din blockmatris som en produkt av och någon annan blockmatris och se vad du får. Du vet att determinanten av är och förhoppningsvis så kommer determinanten av den andra blockmatrisen i produkten då att vara .
Men om produkten blir följande:
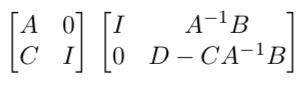
Hur bevisar detta att det(M)=det(A)det(D − CA−1B)?
Determinanten av den första blockmatrisen är och determinanten av den andra blockmatrisen är .
Tack för din hjälp! Men måste man inte på något sätt visa hur man kom fram till det? Det vill säga hur man kom fram till den andra matrisen?
Det räcker nog med att visa att produkten blir den ursprungliga matrisen . Men för att ge lite motivation kring hur vi kommer fram till faktoriseringen av den ursprungliga matrisen så kan vi resonera enligt följande. Eftersom att vi vill komma fram till att determinanten av den ursprungliga matrisen är så väljer vi först någon matris som vi vet kommer ha determinanten , vilket uppfylls av . Vi ska då ha att
,
där är några matriser som vi nu låtsas inte känna till. Enligt räknereglerna för (block)matrismultiplikation får vi då matrisekvationerna
,
,
,
.
Den första ekvationen ger varpå den tredje då ger . Vidare så ger den andra ekvationen att . Då blir den fjärde ekvationen vilket medför .

