cirkelintegral för x dy för halvcirkeln
Hej jag har den här uppgiften (nr17)
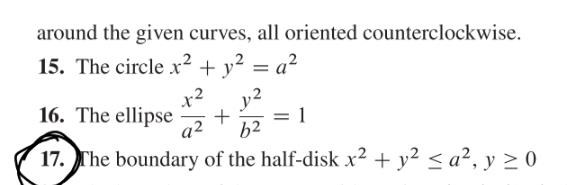
med facit:

I min lösning har jag samma parametriseringar och gränser. Min jacobian blir a och x = acost. Bör inte integralen bli
istället för cos^2t ? Sen så vet jag att man måste ta hänsyn till riktningen men hur implementerar jag det?
Fick du att y=a sin(t)? Vad är derivatan av a sin(t)?
varför skulle jag beräkna derivatan av y ? Är det för att jag gör ett avriabelbyte med y ? men jag tänkte att jaobianen rättar till det (jacobianen = a). Jaha du menar att man skall använda sig av
men blir inte det
solaris skrev:...
men blir inte det
Och vad blir det, när du multiplicerar ihop det?
Blir det inte -0.5
Vad blir ?
Jag skrev ju det. Det är ju skalärmultiplikation. Så a*cost*(-a*sint)+0*(acost) = -a^2costsint = (sintcost = 0.5sin2t) = -0.5*a^2*sin2t.
Har jag fel? För det här är inte samma som i facit. Dvs
Vilken är integralen du skall beräkna? Är det denna?
I facit delar man upp denna integral i två och integrerar fältets -komponent () och fältets -komponent () separat, d.v.s.
När du skall beräkna
får du att (eftersom ). Det ger istället skalärprodukten:
vilket är samma som facit kommit fram till.
Jag måste även nämna ett annat sätt att lösa den här uppgiften, nämligen Greens formel! Jag vet inte om du lärt känna den fullt ut, men den säger nämligen att för en sluten kurva som innesluter området gäller:
I vårt fall är detta väldigt gynnsamt. Eftersom vår kurva definieras som randen till halvcirkelskivan och och ger Greens formel direkt:
Och med så få beräkningar kan vi konstatera att integralens värde är noll!
Tack! jag misade att
:D
solaris skrev:Tack! jag misade att
:D
Just precis.



