Cirkelns ekvation
Fråga: En cirkel tangerar linjen 3x-4y=0 i punkten (8,6). Den tangerar dessutom den positiva x-axeln. Bestäm cirkelns medelpunkt och radie.
Skulle vara väldigt hjälpsamt om någon kunde hjälpa till.
Har du ritat en bild? Vet du hur ekvationen ser ut för en cirkel med radie r och medelpunkt (x0,yo) ser ut?
Jag har ritat linjen y=3/4 x och markerat punkten (8,6) som ligger på y=3/4 X
cirkeln ligger under linjen y=3/4x då den tangerar även x-axeln.
vet inte vad jag ska rita mer
Ok cirkelns ekvation för radie r och medelpunkt (x0,y0) ?
Nej, vet inte hur jag ska rita den om ja inte har fått någon info om den
Jag tänkte bara (x-x0)2+(y-y0)2=r2. Detta är ekvationen för en cirkel med radie r och medelpunkt x0 , y0.
Jaha, ja det vet jag. Men hur tar jag mig vidare?
Så till att börja med (8-x0)2+(7-y0)2=r2 detta får vi ifrån de möts i punkten (8,6). Eftersom då måste cirkelns ekvation vara uppfylld för denna koordinat.
Sen vet vi att i punkten x=x0 , y=0 ska den också vara uppfylld. Detta ifrån att den tangerar x-axeln. Så vet vi att x-koordinatens medelpunkt är denna punkten x0
(x0-x0)2+(0-y0)2=r2 =>0+y02=r2 => y0=r.
Edit: Vi behöver ett samband till. :)
I facit står det:
Där cirkeln och dess tangent ritas in i ett koordinatsystem samt att tangenten och cirkelns radie bildar vinkeln 90 grader
Ok dyker det upp någon Pythagoras sats eller något som kan användas kanske?
Det står bara att
r=10/3
medelpunkt: (10,10/3)
Det ser inte ut som om du har använt det faktum att en linje från tangeringspunkten till cirkelns centrum är vinkelrät mot tangenten (och du vet ju riktningskoefficienten för både linjen och x-axeln och dessuton tangeringspunkten med linjen). Rita!
Om man ritar på denna kan man se att avståndet från origo till skärningspunkten (8,6) är samma som avståndet från origo till cirkelns tangeringspunkt med x axeln. Alltså är x0 lätt beräknad. I och med att den tangerar x-axeln är y0 = r.
Oj det var en arbetsam uppgift, men också en nyttig repetition av flera olika saker.
Det första är att skapa sig en bild av det hela.
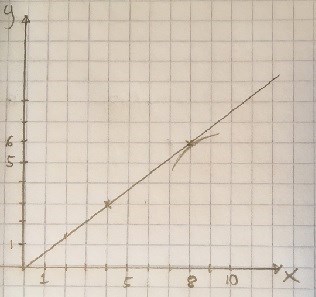 Här har jag ritat linjen från ekvationen och markerat punkt (8;6) Där fick jag idén att vi borde kunna ha en vinkelrät linje genom punkt (8;6) som delar cirkeln mitt itu.
Här har jag ritat linjen från ekvationen och markerat punkt (8;6) Där fick jag idén att vi borde kunna ha en vinkelrät linje genom punkt (8;6) som delar cirkeln mitt itu.
För att få k-värdet på den linjen fick jag leta på ekvationen
Efter lite pysssel så hade jag denna figur
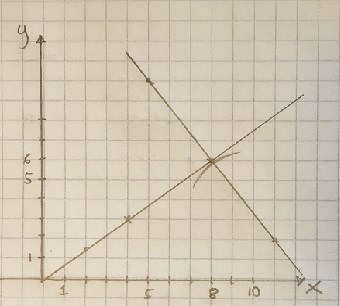 Nu kunde jag rita en ungefärlig cirkel med passaren.
Nu kunde jag rita en ungefärlig cirkel med passaren.
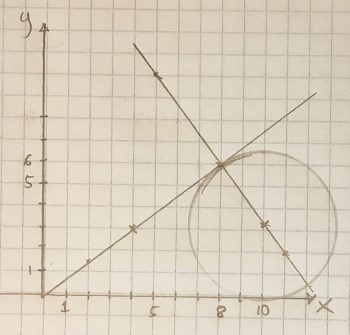 Här började jag ana det AndersW såg att vi har en likbent triangel. Avståndet från Origo till (8;6) borde vara lika stort som avståndet Origo och en punkt på x-axeln. Med pythagoras sats så kan vi få fram det.
Här började jag ana det AndersW såg att vi har en likbent triangel. Avståndet från Origo till (8;6) borde vara lika stort som avståndet Origo och en punkt på x-axeln. Med pythagoras sats så kan vi få fram det.
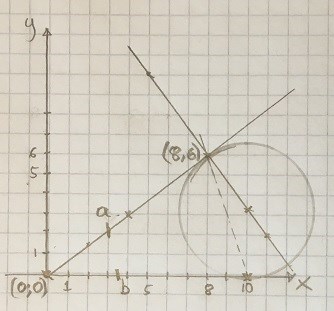 Här ser vi den likbenta triangeln och benen a och b är lika stora.
Här ser vi den likbenta triangeln och benen a och b är lika stora.
Från ändpunkten på linje b så kan vi dra en vinkelrät linje rakt upp och resten är bara arbete.
Hoppas det kan vara till hjälp.
Hej!
Tack för alla svar.
Men jag undrar varför "avståndet från origo till skärningspunkten (8,6) är samma som avståndet från origo till cirkelns tangeringspunkt med x axeln".
Med Connys utsökta bild till hjälp så om vi ritar en radie till x axeln samt en linje från origo till mittpunkten av cirkeln så får vi två trianglar som delar en sida (linjen mellan cirkelns mittpunkt och origo) Vi vet också att dessa trianglar är rätvinkliga (radien är alltid vinkelrät mot en tangent)
Då har vi två rätvinkliga trianglar som delar hypotenusa och har en katet som är lika med radien på cirkeln. Alltså måste de återstående kateterna i trianglarna vara lika långa.
Här har jag ritat in linjen och de räta vinklar Anders beskriver.
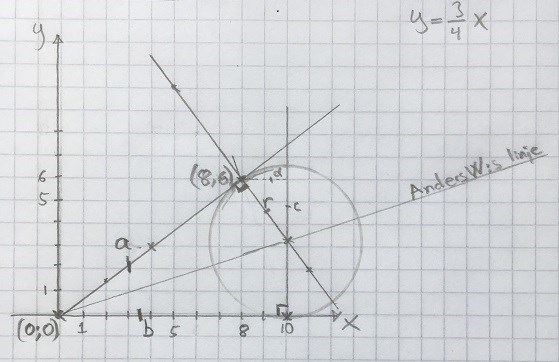
Vi ser också att det vi kallar Anders linje är bisektrisen och oavsett vilken vinkel vi väljer så kommer Anders bevis att hålla.
Även vid större vinklar än 90 grader kommer beviset att hålla.
Det är lätt att se. Vi kan rita tangenten i punkten där bisektrisen skär cirkeln och då har vi en större vinkel än 90 grader mot x-axeln.
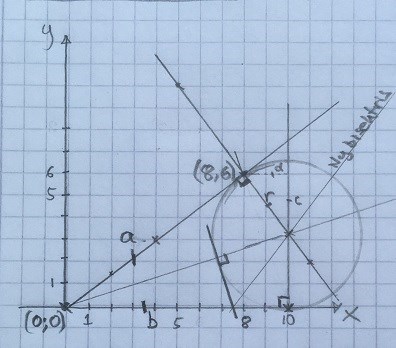
En fråga: Jag håller på med bevis i Matte 4. Vad säger ni som är erfarna, duger det här som bevis?
Alternativ lösning medelst skalärprodukt:
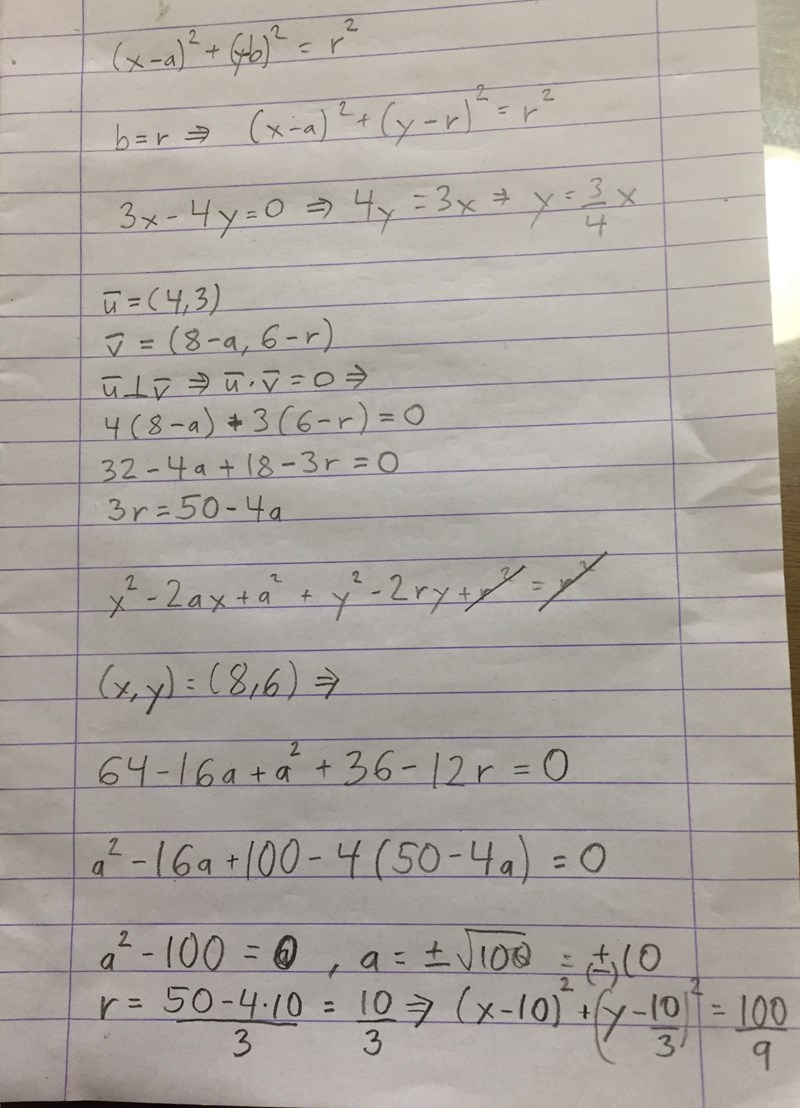
tomast80 skrev:Alternativ lösning medelst skalärprodukt:
Snyggt, men det har man inte lärt sig i Ma3.
tomast80 skrev:
Alternativ lösning medelst skalärprodukt:
Tack tomast80 det var en intressant lösning!
Smaragdalena skrev:tomast80 skrev:Alternativ lösning medelst skalärprodukt:
Snyggt, men det har man inte lärt sig i Ma3.
En fråga jag stör ju den här tråden nu känner jag, men är beviset ovan en godkänd bevismetod?
Bör jag sammanfatta det i en egen fråga i en ny tråd?
Bevis är något jag tycker är oerhört svårt. Bevis i gymnasieläroböcker känns ofta som rena självklarheter, så självklara så beviset blir svårare att förstå än det man försöker bevisa?
Smaragdalena skrev:tomast80 skrev:Alternativ lösning medelst skalärprodukt:
Snyggt, men det har man inte lärt sig i Ma3.
Visserligen, men skalärprodukten lika med noll är ju egentligen samma sak som att:
för vinkelräta linjer, så hade enkelt kunna ändrat lösningen genom sambandet:
Då blir hela lösningen på Ma3-nivå!
Hade denna uppgiften på kunskapsmatrisen för kursen Matematik 2c, men man skulle endast ta fram koordinaterna för mittpunkten. Vad finns det för sätt att lösa den med ma2c-kunskaper? Man lär vara tvungen att ta fram radien oavsett för att få en y-koordinat? Mvh





