differentialekvation
Hej!
Har tenta om ett par dagar. Har fastnat helt och hållet på denna teorifrågan.
" Bestäm en funktion f(x) sådan att och arean under kurvan y(x) mellan 0 och x är proportionell .
En kommentar från läraren ser ut så här:
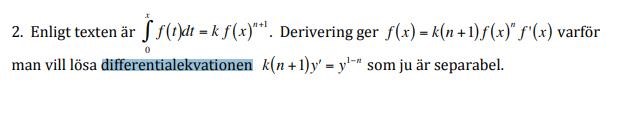 Jag har dock svårt att hitta integralen. Jag har tänkt så här typ:
Jag har dock svårt att hitta integralen. Jag har tänkt så här typ:
Vi vet också att f(0)=0 och f(1)=1
Svaret ska bli
Om mitt resonemang stämmer, hur går man vidare!
Tack!
Din lärare har skrivit HL som , du har skrivit HL som . Varför?
Jag har ändrat det nu! Det var bara första raden som är fel.
Sen det jag gör är att dividera med y^(1-n) för att få det på dy sidan
därefter bryter jag ut en minustecken y^(1-n) =y^-(-1+n) och få upp det på täljaren. Därför blir det y^(n-1)
Du har tappat bort dx i HL på andra raden. På något sätt har du fått dy i HL på tredje raden - så skall det inte vara. Sedan kändes det inte meningsfukkt att försöka förstå mer.
Smaragdalena skrev:Du har tappat bort dx i HL på andra raden. På något sätt har du fått dy i HL på tredje raden - så skall det inte vara. Sedan kändes det inte meningsfukkt att försöka förstå mer.
Nu har jag uppdaterat och fixat till de misstagen och visat lite tydligare hur jag tänkte.
Men jag kommer ändå ingenstans med denna lösningen. Kan du se ett mönster?
Hej!
Texten säger att integralen ska vara proportionell mot funktionen
Derivera båda sidor i denna likhet för att få
Differentialekvationen är separabel och kan skrivas
.
Om så är ekvationen samma sak som
annars är ekvationen samma sak som
Om så ger kravet att och kravet bestämmer konstanten .
Om så är funktionen (för ) och kravet ger kravet , så funktionen för alla ; kravet kan alltså inte uppfyllas. Därför kan fallet inte uppstå.
Albiki skrev:Hej!
Texten säger att integralen ska vara proportionell mot funktionen
Derivera båda sidor i denna likhet för att få
Kan ni visa hur ni tänker? Jag kommer ingenstans!!
Albiki skrev:Differentialekvationen är separabel och kan skrivas
.
Om så är ekvationen samma sak som
annars är ekvationen samma sak som
Om så ger kravet att och kravet bestämmer konstanten .
Om så är funktionen (för ) och kravet ger kravet , så funktionen för alla ; kravet kan alltså inte uppfyllas. Därför kan fallet inte uppstå.
Oki nu känns det lite mer tydligare. Jag måste sitta o lugn och ro och försöka fatta detta steg för steg!
Tack för hjälpen i alla fall!
Dude.96 skrev:Albiki skrev:Hej!
Texten säger att integralen ska vara proportionell mot funktionen
Derivera båda sidor i denna likhet för att få
Kan ni visa hur ni tänker? Jag kommer ingenstans!!
- Om du deriverar med avseende på så får du . Detta är Integralkalylens fundamentalsats.
- Om du deriverar med avseende på x så får du . Detta är Kedjeregeln.