Differentialekvationen fråga
bestäm y' till differentialekvationen 4y''+48y' = - 144y
Såhär gjorde jag
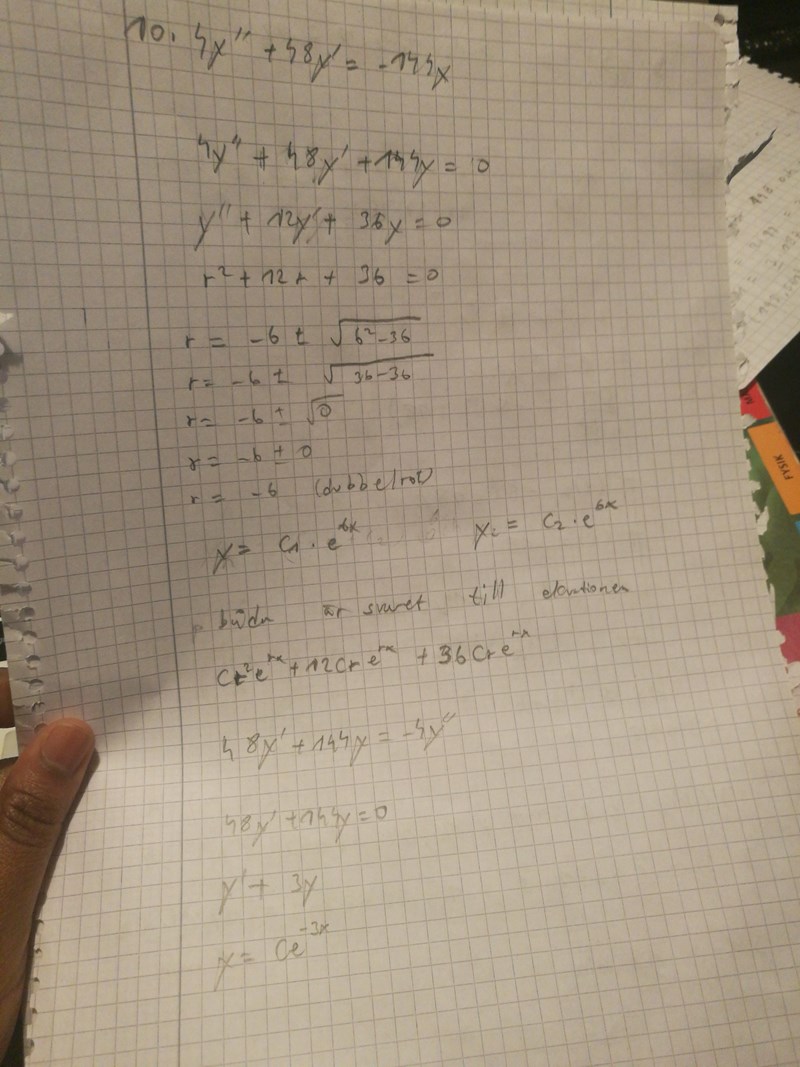
Är det fel? Det går knappt att läsa det du skriver, kom du fram till att var lösningen? Rimligtvis bör du ha kommit fram till att var en lösning.
Dessvärre är inte vad man kallar en fundamental lösning. (Wronskianen är okomplett) och således måste du göra en variation av parametrar. Det går egentligen ut på att du antar att , och till slut kommer du komma fram till att den fundamentala lösningen ges av inte bara utan även , således ges den fundamentala lösningen av .
Jag kom fram till det du skrev nyss om C1 och C2.. Så du menar att lösningen är y = C1*e^-6x +C2*e^-6x. Men vi vet ej vad C1 och C2 är här
Mahiya99 skrev:Jag kom fram till det du skrev nyss om C1 och C2.. Så du menar att lösningen är y = C1*e^-6x +C2*e^-6x. Men vi vet ej vad C1 och C2 är här
Man kräver att en lösning till denna typen av diff.ekvationer har en fundamental (och unik) lösning. Jag skrev däremot fel, du behöver inte göra en variation of parameters här. Men lösningen är inte en fundamental lösning till din diff.ekvation. Vad man gör då är att man ansätter att lösningen istället ges av (man bara tänker att konstanten C egentligen är en funktion av ) och sedan hittar och och sätter in i diff.ekvationen.
Till slut när du gjort allt detta kommer du se att konstanten egentligen är en funktion av , nämligen en funktion som uppfyller , och därmed får du att , din fundamentala lösning ges alltså av , eller bara .
Notera att det är ett i ena men inte i andra.
Ärligt talat vet jag inte om det är meningen att du ska kunna detta i gymnasiet, även fast det är Ma5, så det kanske helt enkelt är meningen att du ska säga .
Ok jag är lite förvirrad här. Men om vi deriverar y = Aex^-6x+be^-6x så får vi y' =-6Ae^-6x-6be^-6x
och andra derivatan y''= 36Ae^-6x+36be^6x. Sedan sätter vi in dem i vår ursprungsfunktion va? Och till slut kommer visaa saker ta ut varandra så vi har termer för lösa ut y'?
I din formelsamling står det förmodligen något om tre olika fall beroende på hur rötterna till den karaktäristiska ekvationen ser ut. De tre fallen är
- Rötterna och är reella och olika
- Rötterna är reella och lika
- Rötterna är komplexa på formen
I fallet med en reell dubbelrot är lösningarna
Ja men vi har aldrig gått igenom såna formler. Dock fick jag att 6 är en dubbel rot
Det blir väl y = e^6x (C+Dx) men vi vet ej vad C respektive D är.
Du fick en negativ dubbelrot,
Alltså är
Deriverar vi y(x) får vi:
Vill man bestämma konstanterna måste man använda ytterligare information, kanske är värden för eller givet. Annars får man tills vidare acceptera att de allmänna lösningarna ges av två okända konstanter.
Jroth skrev:Du fick en negativ dubbelrot,
Alltså är
Deriverar vi y(x) får vi:
Jag tror du skrev fel där. Det ska vara y'(x) = - 6Ce^-6x-6De^x. Nej inget annat är givet i uppgiften än att bestämma y' till differentialekvationen. Så man får svara att y' ges av två okända kontanter ned allmänna lösningar
Nej, derivatan med avseende på x är
Jroth skrev:Nej, derivatan med avseende på x är
Jag hänger inte med hur du fick den deriveringen
Derivatan av en produkt:
Funktionen består av och
Derivatan blir då
Är du med på det?
Jaha du använde derivatan av en produkt? Ok. Jag får dock att deriveran av just Dxe^-6x blir 0*xe^-6x+D*(-6)*xe^-6x
Juste nu förstår jag
Hur får du 0?
Om du valde att dela upp funktionen i och så har du kvar problemet.
Derivatan av är
Jroth skrev:Hur får du 0?
Om du valde att dela upp funktionen i och så har du kvar problemet.
Derivatan av är
Nu när jag tänker efter så var min uppdelning fel, så det korrekta är hur du uppdelade. Tack!


