Dubbelintegral
Hej!
Jag håller på och räknar på en dubbelintegral men jag får inte rätt på det... Här är uppgiften: 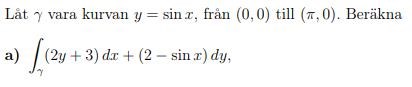
Jag har räknat så här:
Men svaret ska bli 4 + 3pi, hur kommer man fram till det?
Använder du alls kurvans utseende här?
Läs om parametrisering av linjeintegraler.
Ja, hmm det är ju de värdena jag har försökt sätta in som gränser till integralerna... eller är de fel?
Jag ska läsa på :-)
Det här är inte en dubbelintegral, utan en kurvintegral, en integral längs en kurva i .
Av din beräkning att döma tycks du behöva repetera vad en kurvintegral är och hur man beräknar den.
Det är nämligen så att
betyder att du skall beräkna integralen längs kurvan genom vektorfältet . Detta kan du göra på flera olika sätt. Ett alternativ är att använda sig av en parametrisering och formeln:
eller så kan du lägga till ett linjestycke så att kurvan blir sluten och då använda Greens formel för att omvandla den till en dubbelintegral:
Eftersom y är en funktion av x kan du skriva om integralen så att du bara behöver en variabel, x. Vad blir dy?
Nu förstår jag mer hur det här fungerar! Jag har lyckats lösa b) uppgiften (som inte finns med här) men kan fortfarande inte lösa den här...
Det går att se att
Från detta kan man konstatera att kurvintegralen är oberoende av integrationsvägen, det enda som påverkar är kurvans start och slutpunkt. Vi kan alltså tex gå vägen längs x-axeln från 0 till pi.
inför parametriseringen där 0<= t <= pi
men jag löser ut den integralen tycker jag att jag bara får 3pi kvar... ( = osv...)
Ska jag använda en annan metod för att lösa den här uppgiften? Potential till exempel, jag vet inte riktigt hur man använder det?
Detta fält är inte potentialfält (), så det går varken att byta kurva eller beräkna med hjälp av potentialfunktion.
Det går visserligen att använda Greens formel, men det tycker jag krånglar till saker och ting. Jag skulle köra på parametriseringsdefinitionen av en kurvintegral.
Men vad har jag gjort fel? Hur gör man för att få 4 + 3pi?
Kan man verkligen använda Green när dQ/dx - dP/dy = 0?
Ja, Greens formel går att använda även om fältet är ett potentialfält, men det här fältet är inte ett potentialfält. Det gäller alltså inte att .
Jag skulle försöka parametrisera kurvan med en parametrisering och därefter använda formeln:
där och är -värdena som motsvarar kurvans ändpunkter.
Nu har jag löst den! :-)
Det var bara att använda helt vanlig parametrisering, fast med




