ekvationer
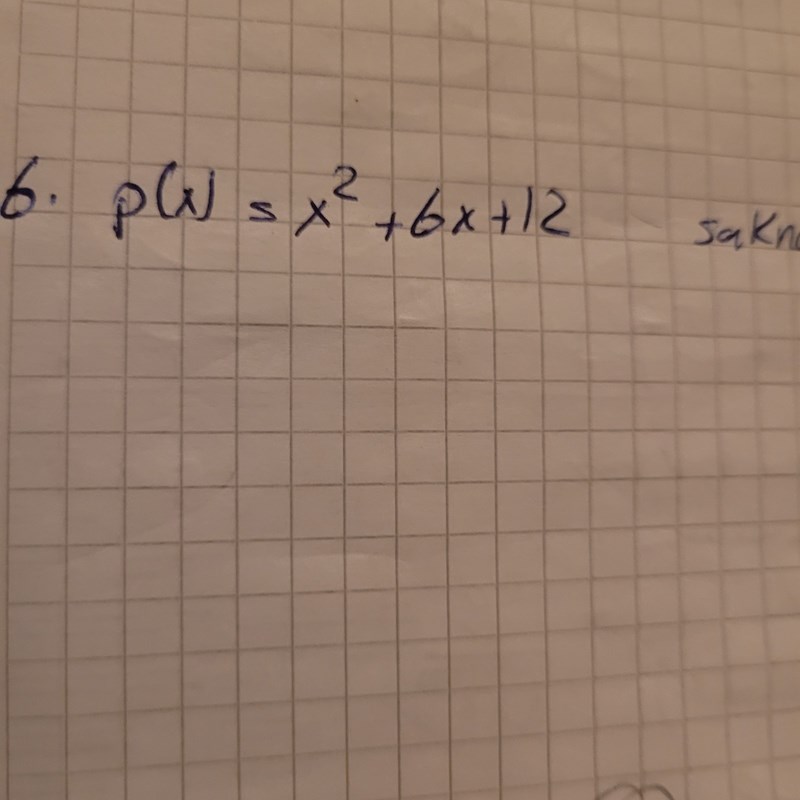 hej behöver hjälp den saknar nollställe man behöver visa detta algebraiskt men ska man sätta men lika med noll p(0) =?
hej behöver hjälp den saknar nollställe man behöver visa detta algebraiskt men ska man sätta men lika med noll p(0) =?
Den saknar mycket riktigt reella nollställen.
Du kan visa detta genom att visa att . Detta eftersom att vi inte kan utföra om x<0 om vi inte introducerar komplexa tal.
Dracaena skrev:Den saknar mycket riktigt reella nollställen.
Du kan visa detta genom att visa att . Detta eftersom att vi inte kan utföra om x<0 om vi inte introducerar komplexa tal.
hur ???? 6/2 ^2 -12?
pq-formeln!
Dracaena skrev:Den saknar mycket riktigt reella nollställen.
Du kan visa detta genom att visa att . Detta eftersom att vi inte kan utföra om x<0 om vi inte introducerar komplexa tal.
ja men ska räkna hur menar du så x^2 +6×+12=0 eller man lösar utan lika med 0 med p.q
pq-formeln säger att:
, men om det som står innanför är negativt så saknar funktionen reella nollställen.
Dracaena skrev:pq-formeln säger att:
, men om det som står innanför är negativt så saknar funktionen reella nollställen.
så man räknar som vanligt med p.q formel
tack så mcyket
Finns ett annat sätt att lösa det också, genom att använda första kvadreringsregeln "baklänges".
p(x) = x^2 +6×+12 kan skrivas som p(x) = +3.
eftersom en kvadrat alltid är positiv (eller noll), och man lägger till 3, så kan p(x) inte bli noll.



