Find a solution to the equation \text{tan}(z) = 5 i which satisfies the condition 0 < Re(z) < \pi.
Find a solution to the equation which satisfies the condition .
Re = reala delen i axeln, x- axeln liksom..
0 <= alalla <= pi, betyde r att vi befinner oss i första och andra kvadraten
tan = sin/cos
5i betyder att vi är på siffran 5 hos 'y" liksom..
jag tänkte om man kunde typ använda arctan på bägge led, men det blir ju fel.
Med hjälp av Eulers formler för sinus och cosinus kan skrivas:
Din ekvation är alltså samma sak som:
Kan du lösa detta?
AlvinB skrev:Med hjälp av Eulers formler för sinus och cosinus kan skrivas:
Din ekvation är alltså samma sak som:
Kan du lösa detta?
Använda log och så?
men nääe,, jag ve tinte :S ååå får sån ångest över , log osv. Och n u med också komplexa tal :S
Det mesta är klurigt till en början, men övning ger färdighet!
Jag tycker vi börjar med att multiplicera båda led med :
Sedan multiplicerar vi med nämnaren:
Se nu vad du får om du förenklar.
AlvinB skrev:Det mesta är klurigt till en början, men övning ger färdighet!
Jag tycker vi börjar med att multiplicera båda led med :
Sedan multiplicerar vi med nämnaren:
Se nu vad du får om du förenklar.
och typ Log:a på bädde sidor
iz-iz = -5(iz-iz)
ehm... näe..
Eftersom så varför blir det konstigt.
Nej, nu har du lite bråttom. Det går inte att använda logaritmer för att trolla bort potenserna på det sättet du gör. Du kanske behöver kika lite grann på logaritmlagarna från Matte 2 på gymnasiet.
Vad jag menade var att du skulle förenkla enligt följande:
Nu kommer ett steg som kan vara lite svårt att komma på själv, men kolla vad som händer om vi multiplicerar båda led med :
Kan du nu lösa ut för ?
AlvinB skrev:Nej, nu har du lite bråttom. Det går inte att använda logaritmer för att trolla bort potenserna på det sättet du gör. Du kanske behöver kika lite grann på logaritmlagarna från Matte 2 på gymnasiet.
Vad jag menade var att du skulle förenkla enligt följande:
Nu kommer ett steg som kan vara lite svårt att komma på själv, men kolla vad som händer om vi multiplicerar båda led med :
Kan du nu lösa ut för ?
det lär väl bli ngt med:
använder log i båda led:
men vet inte hur det blir med där..
Nja, det blir:
Om du nu tar naturliga logaritmen av båda led får du:
Har du beräknat logaritmen av ett negativt tal förut?
AlvinB skrev:Nja, det blir:
Om du nu tar naturliga logaritmen av båda led får du:
Har du beräknat logaritmen av ett negativt tal förut?
nää, det går ju inte.. inte i den reala mattevärlden. Men iofs, då ska ma ju använda
log(−1)=(2𝑛+1)𝜋𝑖,𝑛=0,±1,... som jag hittade i min bok.
Så mitt blir då
log(-2/3) = (2𝑛+2/3)𝜋𝑖,𝑛=0,±1,. right? så..
2iz = (2𝑛+2/3)𝜋𝑖,𝑛=0,±1. dela med två
iz = 1/2((2𝑛+2/3))𝜋𝑖,𝑛=0,±1 multiplicera med i. i^2 = -1
-z = i(1/2((2𝑛+2/3))𝜋𝑖,𝑛=0,±1) multiplicera med -1
z = -i(1/2((2𝑛+2/3))) 𝜋𝑖,𝑛=0,±1
och eftersom villkoret är 0 till första kvadraten, så ska jag bara kolla de 𝑛 värden som är inom det intervallet?
Du är på rätt spår.
Det stämmer att:
eftersom (och när man lägger på heltalsmultipler av till argumentet ändras ju inte värdet). Dock blir det lite fel när du skall ta fram . Du skall använda dig av logaritmlagen som säger att . Vi får alltså:
Vad får du då för -värde?
kan du bestämma genom att du vet att realdelen av skall ligga mellan och .
AlvinB skrev:
Du är på rätt spår.
Det stämmer att:
eftersom (och när man lägger på heltalsmultipler av till argumentet ändras ju inte värdet). Dock blir det lite fel när du skall ta fram . Du skall använda dig av logaritmlagen som säger att . Vi får alltså:
Vad får du då för -värde?
kan du bestämma genom att du vet att realdelen av skall ligga mellan och .
Det är tyvärr fel. Visa hur du kommer fram till det svaret, så kan vi hitta var det blir fel.
AlvinB skrev:Det är tyvärr fel. Visa hur du kommer fram till det svaret, så kan vi hitta var det blir fel.
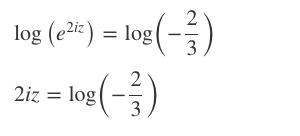
jag måste dividera båda led med 2.
sen:
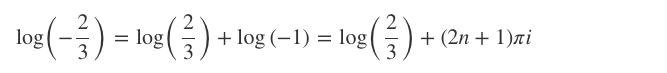
log lagarna:
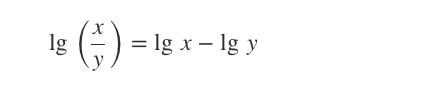
log(2/3) = log(2)-log(3)
så summerar man allt detta i ett , så fick jag min ekvation
Jo, men vad händer med :et i vänsterled?
AlvinB skrev:Jo, men vad händer med :et i vänsterled?
mja men då tar jag det svaret jag hade, och multiplicerar i på båda sidor, och har i minne att
så:
Fortfarande lite knas. Om jag börjar kanske vi hamnar på rätt spår:
AlvinB skrev:Fortfarande lite knas. Om jag börjar kanske vi hamnar på rätt spår:
och så kolla n värderna?
Just det.
AlvinB skrev:Du är på rätt spår.
Det stämmer att:
eftersom (och när man lägger på heltalsmultipler av till argumentet ändras ju inte värdet). Dock blir det lite fel när du skall ta fram . Du skall använda dig av logaritmlagen som säger att . Vi får alltså:
Vad får du då för -värde?
kan du bestämma genom att du vet att realdelen av skall ligga mellan och .
Det är den sista där, att hitta värdarna, asså vart den går upp till?
Rätt svar är:

(har btw, tagi tupp den här kursen igen, sådärav jag kommer såhär 300 år senare)
för blir förvirrad när vi har är ju van liksom vid heltalen.
Övrigt, så har jag stött på:

Är det ngt jag kan tillämpa på min uppgift också?
Ja, det är väl svaret vi kommit fram till?
Vi kom ju fram till:
vilket vi på lite snyggare form kan skriva:
Eftersom vi har villkoret måste vi ha (med blir och med blir ). Detta ger:
vilket är ekvivalent med facits svar.
Du tar fram definitionen för en kurvintegral i det komplexa talplanet, men det har inget med denna uppgiften att göra. Det står ju ingenting om någon integral i uppgiften, eller hur?
AlvinB skrev:Ja, det är väl svaret vi kommit fram till?
Vi kom ju fram till:
vilket vi på lite snyggare form kan skriva:
Eftersom vi har villkoret måste vi ha (med blir och med blir ). Detta ger:
vilket är ekvivalent med facits svar.
Du tar fram definitionen för en kurvintegral i det komplexa talplanet, men det har inget med denna uppgiften att göra. Det står ju ingenting om någon integral i uppgiften, eller hur?
jaaaa okej jag tänkte summa.. shit ok! Aa tack! ska testa lite mer ;)


