Geometri
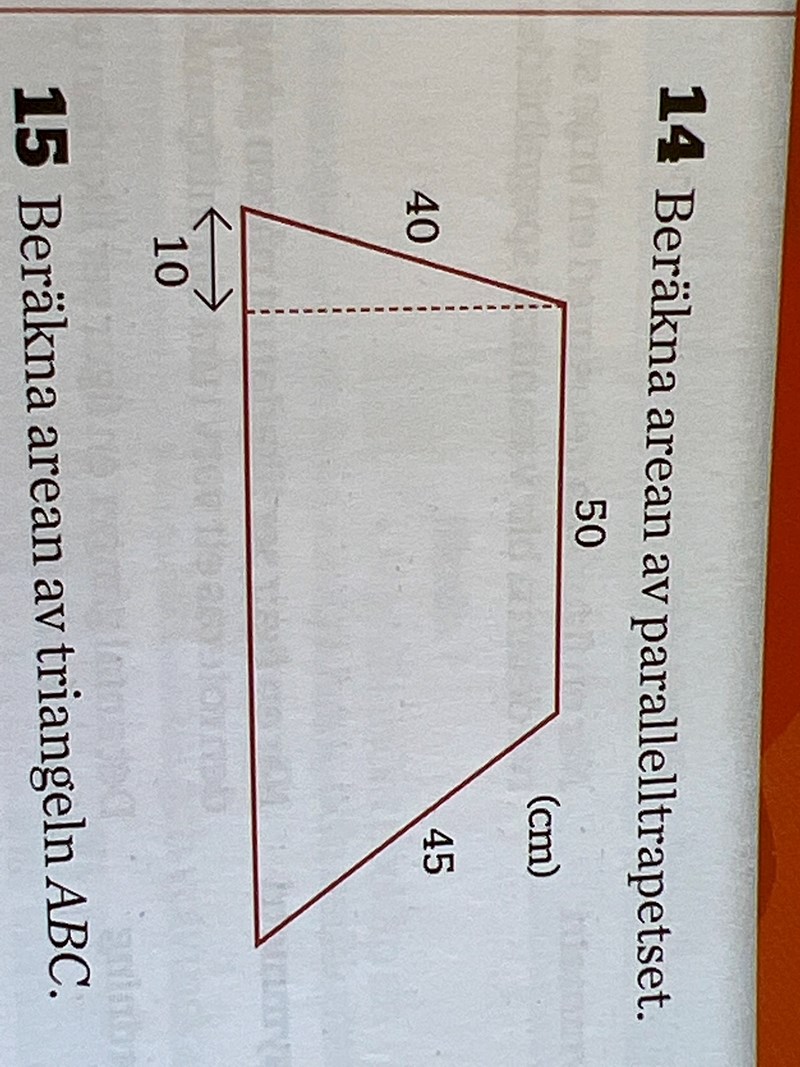 hej! Jag har fastnat på denna fråga. Jag tar 45/40=1,125
hej! Jag har fastnat på denna fråga. Jag tar 45/40=1,125
1,125 x 50 = 56,25
56,25 x 45 = 2531,25 och så kommer jag inte så långt. Svaret i facit är 2574:)
Vad är det du beräknar när du räknar ut 45/40?
Vilken formel använder man för att beräkna arean av ett parallellogram patrallelltrapets? Vad vet du? Vad behöver du ta reda på?
EDIT: Rättade felskrivning
Instämmer i Smaragdalenas första fråga, men det var väl ett parallellTRAPETS vi skulle bestämma arean av?
Kan du hitta ett sätt att bestämma höjden i trapetset (det är den streckade linjen i fig.)? Den kan du sedan använda den för att bestämma den längsta av de två parallella sidorna.
Ja, då kan man väll använda sig av Pythagoras sats för att få ut den andra sidan.
jag tog 45/40 för att se skillnaden:)
Då blir formeln h(50+x)/2. Och höjden var då 42 ungefär.
Genom Pythagoras sats fick jag fram höjden vilket var 41 (inte 42) och då delade jag in den andra triangeln som ni ser på bilden. Med Pythagoras sats fick jag fram kateten.
40*40 + 10*10 = 41,2*41,2
41,2^2 - 45^2 = 18^2
18+10+50 = 78 (b)
50 (a)
41,2(50+78)/2= 2636,8 vilket inte heller stämmer.
Hur lång är basen? Den består av en del som är 10 cm, en som är 40 cm och en som är en katet i en rätvinklig triangel där du vet hypotenusan och har räknat fram höjden. Avrunda inte hypotenusan, utan räkna med det exakta värdet - det skall ju kvadreras så då blir det enklasiffror.
Jag har gjort det, det var 18:)
Det är den längsta sidan i triangeln som är 40 cm. Höjden måste vara mindre än så.
Förlåt men jag förstår inte vad du menar. Menar du triangeln som dem redan har ”ritat” eller den som har hypotenusan 45?
Triangeln där en sida är 10 och en är 40. Höjden måste vara kortare än hyptenusan.
Jag fick ny svar vilket är 38,7:)
Då får du ett annat värde på delen längst till häger också.
Men gud tack så jättemycket!!!! Jag fick fram svaret:D



