Greens formel - enhetscirkeln

Hej! Har fastnat på följande uppgift.

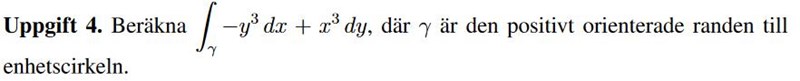
Greens formel ger att integralen är lika med $\int \int_{D} (3 x^{2} + 3 y^{2}) d x d y$ . Men jag hittar inte det nya området! Vi kan ju göra om till polära koordinater och få $x = \cos t, y = \sin t$ för $0 \leq t \leq 2 π$ . Man då är det en enkelintegral, ingen dubbelintegral, eftersom vi bara har 1 variabel att integrera (då radien är konstant). Så kan man väl inte göra? Vi kan väl heller inte sätta $- 1 \leq x \leq 1, - 1 \leq y \leq 1$ eftersom det är en cirkel och inte en fyrkant som integreras. (Svaret ska vara $3 π / 2$ .)

Hej!

Det stämmer att en parametrisering av enhetscirkeln ges av $x=\cos{t}$ och $y=\sin{t}$ . Varför?

Vad är en parametrisering av cirkeln med mittpunkt i origo och radie $R\in\left(0,1\right)$ ?

Vad händer om vi ritar ut alla cirklarna i ett och samma koordinatsystem?

Vi kan även skriva parametriseringen som $x = r \cos t, y = r \sin t$ . Men här är ju r = 1, alltså konstant. Vi kan väl inte låta $0 \leq r \leq 1$ , vi har ju bara att göra med cirkelns rand och inte dess innehåll.

Faxxi skrev:
Vi kan även skriva parametriseringen som $x = r \cos t, y = r \sin t$ . Men här är ju r = 1, alltså konstant. Vi kan väl inte låta $0 \leq r \leq 1$ , vi har ju bara att göra med cirkelns rand och inte dess innehåll.

Poängen med Green's är ju att gå från en kurvintegral till en dubbelintegral (eller tvärtom). Det betyder att din kurva $\gamma$ i kurvintegralen utgör randen till områden $D$ som du sedan integrerar över, dvs. $\gamma=\partial D$ . Så jag tycker det verkar rimligt att låta $0\leq r\leq 1$ för att tillsammans med $\theta\in\left[0,2\pi\right)$ beskriva området $D$ .

Du har rätt! Då är jag med, tack!

Svara Avbryt

Visa senaste svar