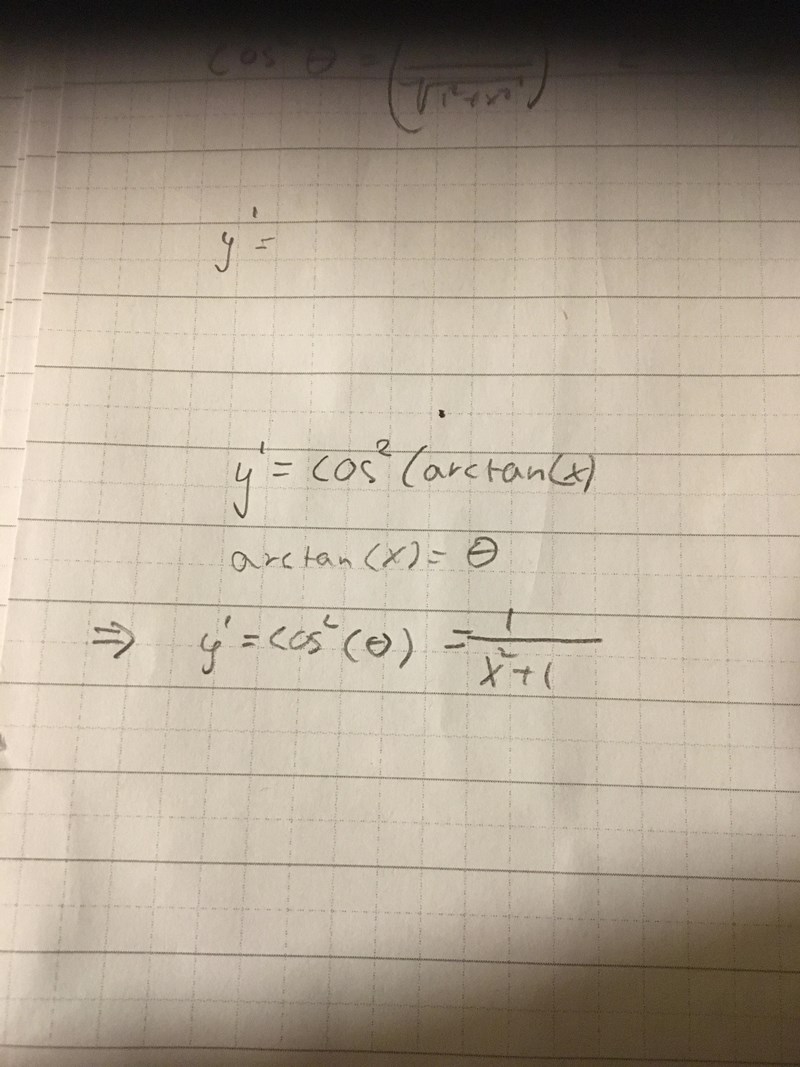11
svar
485
visningar
Liddas är nöjd med hjälpen
Härled derivatan för arctan(x)
 jag kommer såhär långt sen är jag fast!
jag kommer såhär långt sen är jag fast!
, vad blir då?
Vad var A lika med? :)
:), ok 1/(rotenur (x^2+1))
Vi vet att . Alltså är . Kan du fortsätta härifrån?
Vad är då ?
Är lite förvirrad, ser ut som att jag har svaret fast de står cos^2(täta)
Kan du visa att ?
Aha, det är väl det jag har visat?