Hinkens volym

Varför skulle man vilja beräkna volymen för en hink utan att använda formeln för en stympad kon?

Smaragdalena skrev:

Varför skulle man vilja beräkna volymen för en hink utan att använda formeln för en stympad kon?

Det går utöver min intelligens men det är så uppgiften lyder :p

Då får du "förlänga" hinken så att den blir en kon och beräkna volymen för de två konerna och subtrahera.

Smaragdalena skrev:

Varför skulle man vilja beräkna volymen för en hink utan att använda formeln för en stympad kon?

Jag förlängde 18 till 20 och 22 till 20 

och räknade volymen av en cylinder, funkar inte det?

Hur hög blir konen som hinken förvandlas till om man förlänger den?

Smaragdalena skrev:

Hur hög blir konen som hinken förvandlas till om man förlänger den?

Jag förstår inte riktigt vad du menar såhär tänkte jag:

Botten av hinken = 18 i diameter (cm)

Toppen av hinken = 22 i diameter (cm)

Om jag adderar 2 till 18 och subtraherar 2 till 22 så blir det 20,20

Och räknar som om det vore en vanlig cylinder borde inte volymen vara den samma?

pi x 10 x 10 = 314,15...

314,15... x 26 = 8618 cm3

8618 ml = 8,6 Liter

stämmer detta?

Jag förstår inte alls vad du gör. Nej, det blir inte samma sak som en cylinder (men det kan ge ett värde som är "bra nog", det beror på hur exakt man behöver vara).

Standardfråga 1a: Har du ritat?

Smaragdalena skrev:

Jag förstår inte alls vad du gör. Nej, det blir inte samma sak som en cylinder (men det kan ge ett värde som är "bra nog", det beror på hur exakt man behöver vara).

Standardfråga 1a: Har du ritat?

Ja jag har ritat, och jag kontrollerade med att göra med formel för en stympad kon ändå och fick ungefär samma siffra ("bra nog") men jag avrundade pi värdena jag gångrade

professorx skrev:

Smaragdalena skrev:

Hur hög blir konen som hinken förvandlas till om man förlänger den?

Jag förstår inte riktigt vad du menar såhär tänkte jag:

...

Du skrev höjd 24 i uppgiften men räknade med höjd 26.

Smaragdalena menar så här:

Lägg till en kon med höjd x under hinken (se bild).

Den sökta volynen är då (Volym av kon med höjd x+24) - (Volym av kon med höjd x).

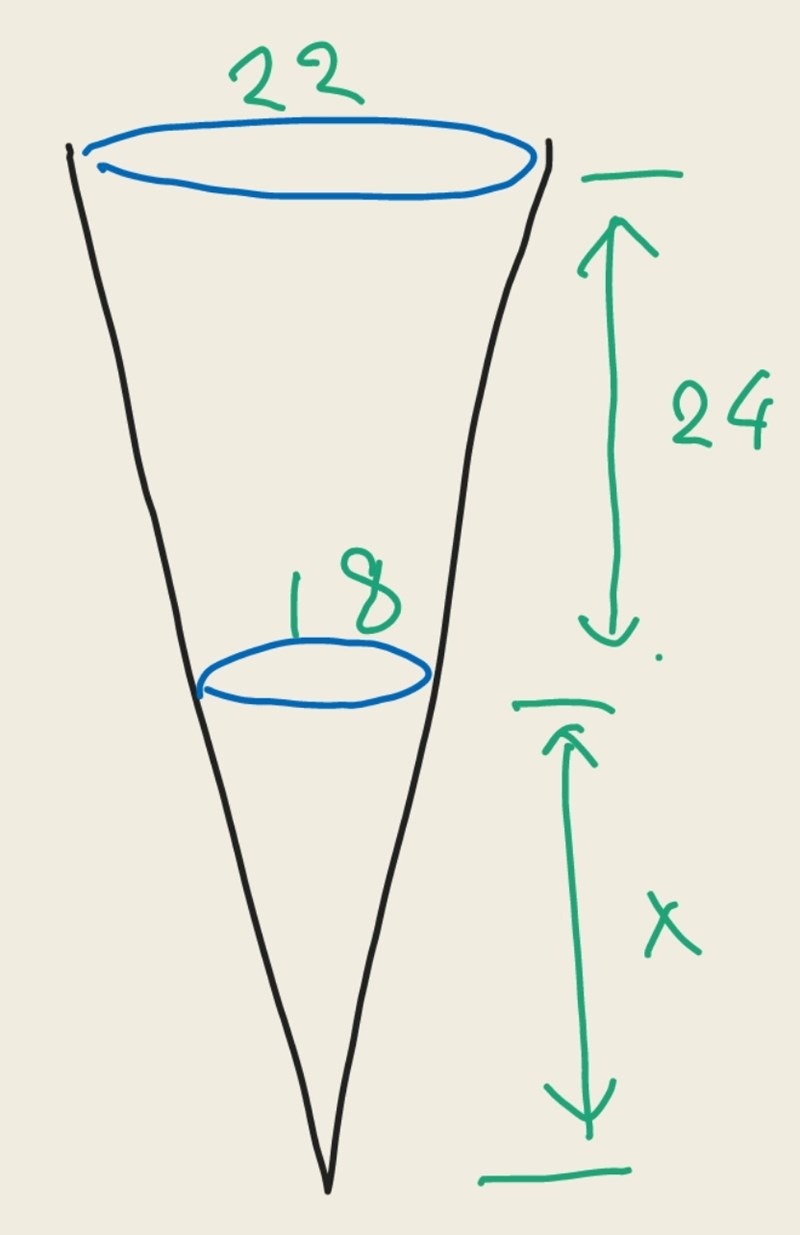
Du har säkert redan räknat ut svaret med hjälp av ovan.

Skillnaden i volym mellan konen med höjden 24+h och volymen av konen med höjden h borde ge dig hinkens volym.

Jobba med med förhållanden mellan trianglarna ABE och CDE för att räkna ut h.

$$\begin{gathered} \frac{\left|AB\right|}{\left|AE\right|}=\frac{\left|CD\right|}{\left|CE\right|} \\ \frac{22/2}{24+h}=\frac{18/2}{h} \\ 11h=216+9h \\ h=108 \end{gathered}$$

Nu är det bara att räkna ut skillnaden på konernas volym:

$H_V=\left(\frac{\mathrm{\pi }·{11}^2·132}{3}\right)-\left(\frac{\mathrm{\pi }·9^2·108}{3}\right)\approx 7565$