Hur göra 5^3x x 2^x = 250^1/2

Hej.

förstår inte hur jag ska lösa:

5^2x x 2^x= 250^1/2

försökte skriva om med basen e:

e^{2x ln 5} x e^{x ln 2} = e^{1/2 ln 250}

2x ln 5 x x ln 2 = 1/2 ln 250

men vet inte hur det ska hjälpa mig..

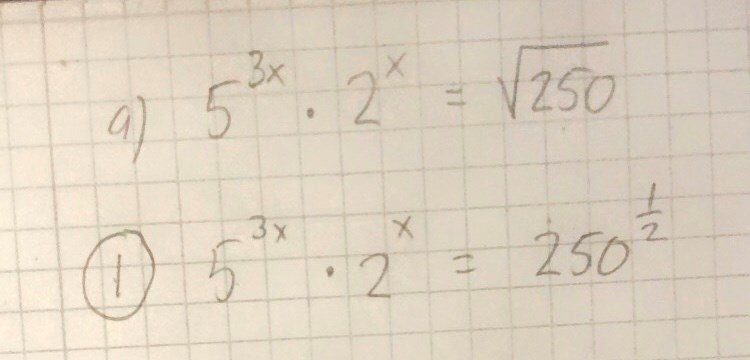
Använd inte "x" både som variable och som multiplikationstecken, det blir väldigt svårläst! Jag brukar skriva ett "." och göra det fett och upphöjt, så att det blir "^.", men om man tycker det är för jobbigt kan man använda * som multiplikationstecken.

I den här uppgiften skulle jag börja med att skriva om HL så att det består av potenser av 5 och av 2. I bästa fall blir det nånting snyggare då (jag har inte testat än).

Du kan ju använda dig av att $\ln (a b) = \ln (a) + \ln (b)$

Vet du hur du kommer vidare då?

Alternativt lös med smaragdlenas tips, det går bra! Jag har provat, och löst den så!

beerger skrev:
Du kan ju använda dig av att $\ln (a b) = \ln (a) + \ln (b)$

Vet du hur du kommer vidare då?

Alternativt lös med smaragdlenas tips, det går bra! Jag har provat, och löst den så!

Vet inte hur jag ska gå vidare från dethär?

hur kan jag använda den räkneregeln när jag har ett multiplikationstecken emellan?

$e^{\ln (5^{3 x})} = 5^{3 x}$ $\neq \ln (5^{3 x})$ (med andra ord, steg 3 är felaktigt)

Blanda in e, använd ln direkt.

Det du har gjort är bara en omskrivning. Du har inte ändrat något värde i VL.

Det blir lite som att försöka lösa $x - 10 = 100$ genom att skriva:

$\frac{2 x}{2} - \frac{20}{2} = 100$

Jag skulle ha gjort samma omskrivning som du i steg 2, men i steg 3 behöver du använda att e^a.e^b = e^a+b där a = ln5^.3x och b = ln2^.x. Sedan, när du bara har ett e på varje sida, kan du logaritmera båda led.

Ser ingen anledning till att blanda in e. Lös med ln direkt.

Ännu ett alternativt sätt att lösa uppgiften på:

$5^{3x}=125^x$

Så vi kan skriva allt som

$250^x=5\sqrt{10}$ och nu kan du ta logaritmen med basen 250 så är du klar. ;)

Logaritmera direkt går bra.

Visa spoiler

5^{3 x} \cdot 2^{x} = \sqrt{250} \ln (5^{3 x} \cdot 2^{x}) = \ln (\sqrt{250}) A n v ä n d \ln (a b) = \ln (a) + \ln (b) \ln (5^{3 x}) + \ln (2^{x}) = \ln (\sqrt{250}) A n v ä n d \ln (x^{y}) = y \cdot \ln (x) 3 x \cdot \ln (5) + x \cdot \ln (2) = \ln (\sqrt{250}) x (3 \cdot \ln (5) + \ln (2)) = \ln (\sqrt{250}) x = \frac{\ln (\sqrt{250})}{3 \cdot \ln (5) + \ln (2)} = \frac{\ln (\sqrt{250})}{\ln (5^{3}) + \ln (2)} = \frac{\ln (\sqrt{250})}{\ln (125) + \ln (2)} = \frac{\ln (\sqrt{250})}{\ln (250)} = = \frac{\ln (250^{\frac{1}{2}})}{\ln (250)} = \frac{\frac{1}{2} \cdot \ln (250)}{\ln (250)} = \frac{1}{2}

beerger skrev:
Ser ingen anledning till att blanda in e. Lös med ln direkt.

Det är en smaksak. Olika människor tänker på lite olika sätt.

Jag tycker att förslaget given av Smaragdalena och Beerger är bra. Jag tycker TS skall kunna alla metoder som finns i tråden men kan självklart lösa uppgiften på de sätt hen föredrar. Personligen så föredrar jag att göra som Smaragdalena tipsade om i sitt första inlägg om jag kan se det. Annars blir det nog ln som gäller för min del. :)

Dracaena skrev:
Ännu ett alternativt sätt att lösa uppgiften på:

$5^{3x}=125^x$

Så vi kan skriva allt som

$250^x=5\sqrt{10}$ och nu kan du ta logaritmen med basen 250 så är du klar. ;)

Detta är ju det allra snabbaste sättet! Går dessutom att lösa med vanliga ln, då du kan lösa 1/2 och sen se att logaritm-termerna tar ut varandra. Så vilken bas du väljer till logaritmen spelar egentligen ingen roll.

Absolut, det går bra med den naturliga logaritmen också. :)

Svara Avbryt

Visa senaste svar