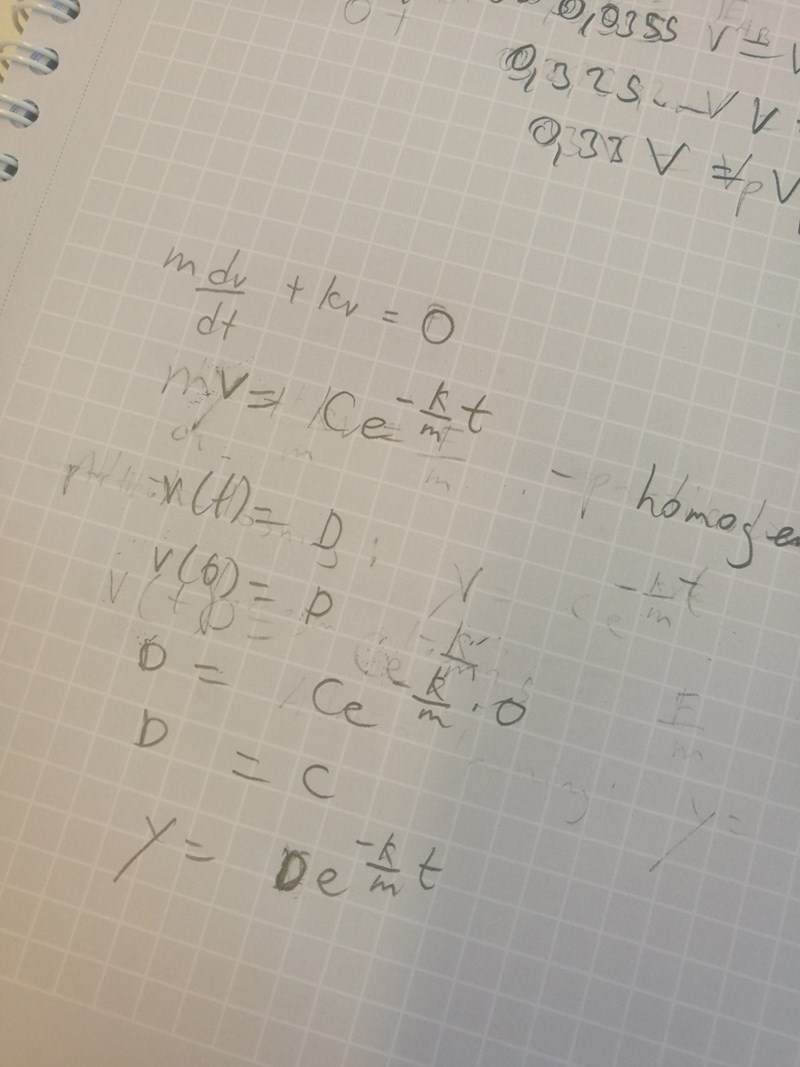jag har dv/dt=F-kv/m
Men jag undrar om ni har tips på hur jag ska tänka vidare?
Mahiya99 skrev:jag har dv/dt=F-kv/m
Men jag undrar om ni har tips på hur jag ska tänka vidare?
Nej, det har du inte - parenteser är viktiga!
Smaragdalena skrev:Mahiya99 skrev:jag har dv/dt=F-kv/m
Men jag undrar om ni har tips på hur jag ska tänka vidare?
Nej, det har du inte - parenteser är viktiga!
Ja dv/dt= (F-kv) /m?
Jag söker tiden och det är där jag har fastnat. Allt annat är ju givet
Jag blir lite nyfiken, vad står den blå bokstaven c för under uppgiftsnumret?
Hursomhelst, jag tycker du ska lösa differentialekvationen med hjälp av en integrerande faktor. Eventuellt kan det vara lättare att inse vilken faktor man kan använda om man skriver om ekvationen
D4NIEL skrev:Jag blir lite nyfiken, vad står den blå bokstaven c för under uppgiftsnumret?
Hursomhelst, jag tycker du ska lösa differentialekvationen med hjälp av en integrerande faktor. Eventuellt kan det vara lättare vilken faktor man kan använda om man skriver om ekvationen
Hm jag är ej med på vad du gör nu.. Varför kan man ej lösa med differentialekvationer eftersom området avser detta? Det blir ganska rörigt för mig om vi går in på integraler. Vill gärna hålla mig inom diff området!
Du kan skriva ekvationen som
m + = .
Bestäm den allmänna lösningen genom att hitta homogen lösning plus en partikulärlösning.
Utnyttja sedan att v(0) = 1,5 m/s för att bestämma obestämda konstanter i den allmänna lösningen.
PATENTERAMERA skrev:Du kan skriva ekvationen som
m + = .
Bestäm den allmänna lösningen genom att hitta homogen lösning plus en partikulärlösning.
Utnyttja sedan att v(0) = 1,5 m/s för att bestämma obestämda konstanter i den allmänna lösningen.
Har jag tänkt rätt?
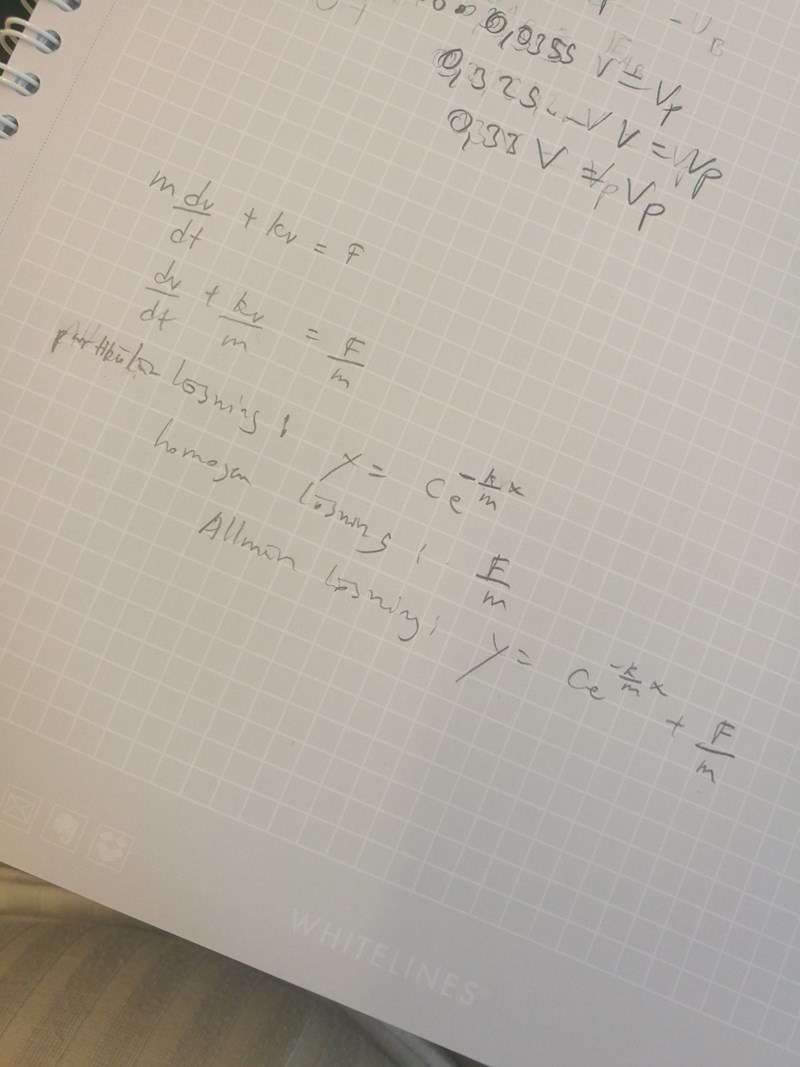
Det är nästan rätt, men du har bytt namn på homogen- respektive partikulärlösning. Den homogena lösningen är alltså lösningen till ekvationen
Och det är den som är . Du har missat ett i exponenten också (eller ja, du använder x och y istället för v och t och det får man såklart göra, men det kan bli lite förvirrande :))
Dessutom har konstanten blivit lite fel i partikulärlösningen. För att hitta rätt konstant kan du ansätta partikulärlösningen
Där bara är en konstant. Om du sätter in i det i differentialekvationen får du ett värde på .
D4NIEL skrev:Det är nästan rätt, men du har bytt namn på homogen- respektive partikulärlösning. Den homogena lösningen är alltså lösningen till ekvationen
Och det är den som är . Du har missat ett i exponenten också (eller ja, du använder x och y istället för v och t och det får man såklart göra, men det kan bli lite förvirrande :))
Dessutom har konstanten blivit lite fel i partikulärlösningen. För att hitta rätt konstant kan du ansätta partikulärlösningen
Där bara är en konstant. Om du sätter in i det i differentialekvationen får du ett värde på .
Är ej v(t) =F/m??
Nej, det kommer visa sig att partikulärlösningen är konstanten
Och den hittar du genom att "chansa" på att (där D är en konstant vars derivata är 0) och sätta in det i differentialekvationen. Testa får du se :)
D4NIEL skrev:Nej, det kommer visa sig att partikulärlösningen är konstanten
Och den hittar du genom att "chansa" på att (där D är en konstant vars derivata är 0) och sätta in det i differentialekvationen. Testa får du se :)
Förstår tyvärr ej varför v(t) =F/k. Men jag testar!
Alltså, vi sätter in ansatsen till partikulärlösning i den ursprungliga diff.ekvationen (inte den homogena ekvationen)
Är du med?
D4NIEL skrev:Alltså, vi sätter in partikulärlösningen i den ursprungliga diff.ekvationen (inte den homogena ekvationen)
Är du med?
Jag tror jag är med nu.
Så nu har du
1) En homogen lösning, dvs en lösning som uppfyller
2) En partikulär lösning, dvs en lösning som uppfyller
Om du lägger ihop lösningarna får du den allmänna lösningen till differentialekvationen.
Slutligen behöver du också bestämma konstanten .
Det gör du genom att undersöka begynnelsevillkoret , dvs hastigheten i ett visst ögonblick enligt uppgiftstexten.
När det är gjort har du en lösning som du kan använda för att bestämma vilket är den egentliga frågan.
v(t) = Ce^-k/mt+F/k?
Jaa, fast du måste som sagt använda begynnelsevillkoret för att bestämma
D4NIEL skrev:Jaa, fast du måste som sagt använda begynnelsevillkoret för att bestämma
Ja juste nä vi är ej klara än, ville bara visa att jag har skapat en allmän lösning nu
Mahiya99 skrev:
Ja juste nä vi är ej klara än, ville bara visa att jag har skapat en allmän lösning nu