Integral av volym

Finns det en bild som hör till uppgiften? En skål som är 15 cm i diametern i toppen, 7,5 cm i botten och 10 cm hög kan se ut påmånga olika sätt, och kan ha mycket varierande volym.

Kan du länka till tråden du hittat och förklara vad du inte förstår, så att vi inte behöver göra om samma uträkningar?

 Är det denna tråd du menar?

Om ja, är din uppgift likadan som i den tråden?

Precis yngve!

 https://www.pluggakuten.se/trad/skalens-volym-med-hjalp-av-integral/

Jag har ju fått för mig att ska jag beräkna arean ovanför kurvan måste jag ta övre funktionen - nedre. Där den övre funktionen ges av y=10 och den nedre av kurvan som jag får. Vill jag sedan att kurvan skall gå igenom en finns punkt ska väl en konstant adderas till integralen?

För att överhuvud taget kunna räkna på detta behöver du ta fram en funktion som beskriver skålens form. Hur ser den ut?

Kan du approximera den med en parabel?

I så fall blir det mycket enklare, se tråden.

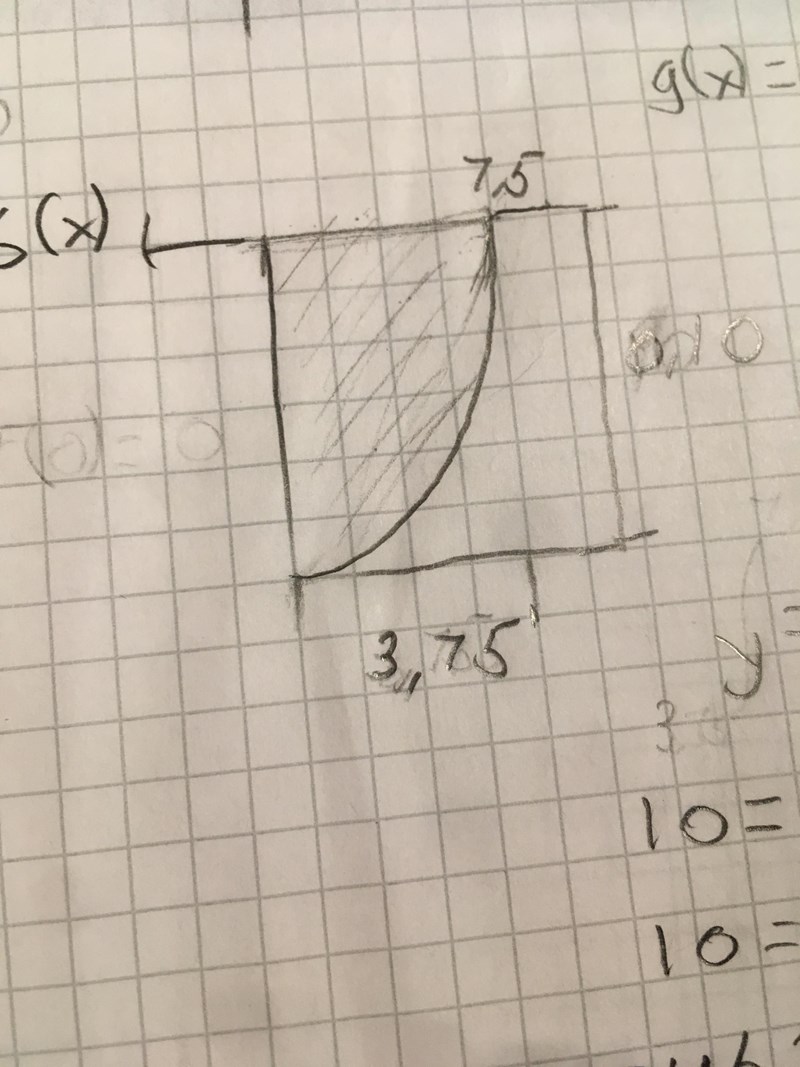
Cylindern har jag inte ritat med för den är det väl bara att addera med arean av denna sedan. 

Davidos skrev :

Cylindern har jag inte ritat med för den är det väl bara att addera med arean av denna sedan. 

Snygg figur, men det går inte att från den se hur skålens bottenyta ser ut eller hur funktionsuttrycket ska se ut.

Kan du rita ut hela skålen i genomskärning, med koordinataxlar och de olika måtten utsatta?

Och en annan fråga, känner du till hur skivmetoden fungerar?

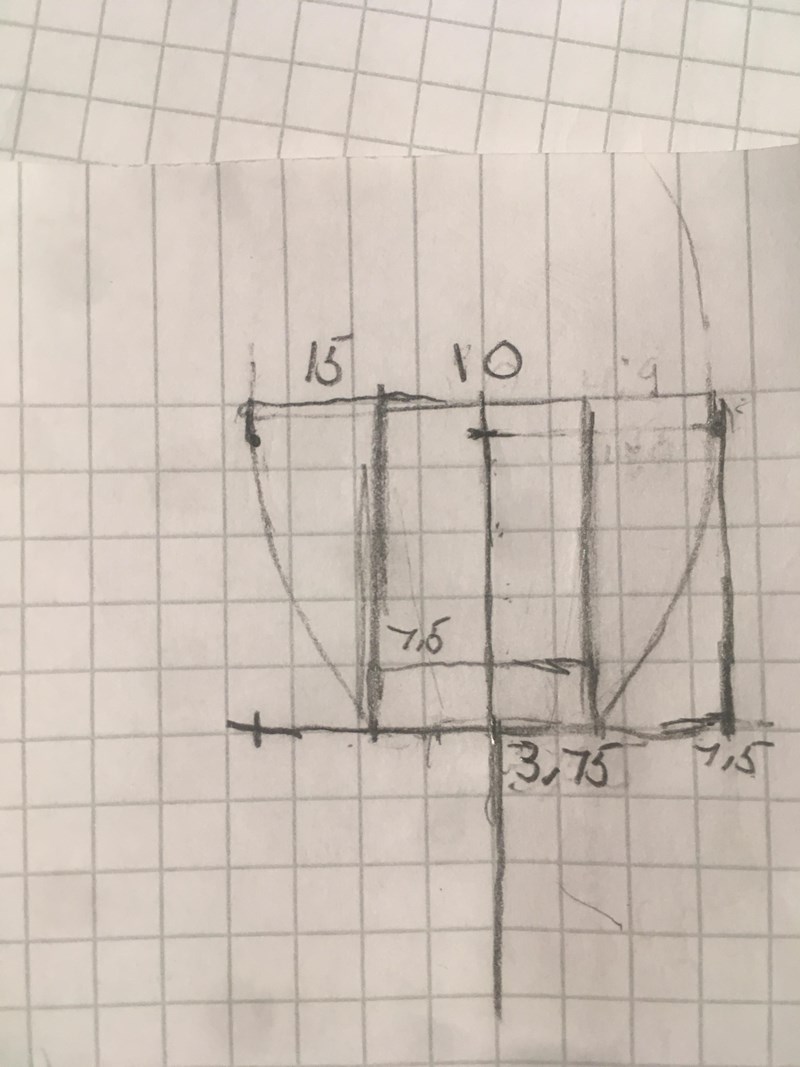Jag vet, konstnär 🙋‍♂️ Joo skivmetoden är väl att man delar upp en integral i mindre delar. Sedan lägger man ihop dessa.

Davidos skrev :

Jag vet, konstnär 🙋‍♂️ Joo skivmetoden är väl att man delar upp en integral i mindre delar. Sedan lägger man ihop dessa.

OK bra.

Börja med att anpassa en andragradskurva y = ax^2 + bx + c så att den passar till kurvan då y > 0.

Tips: symmetrilinjen är x = 0 och du har två punkter på kurvan, nämligen (3,75 : 0) och (7,5 : 10).

Det är här det tar stopp, jag vet att man kan stoppa in värden i den funktionen för att få fram y-värden. 

Men vet inte vart jag skall börja med ax^2+bx+c. Helt förträngt det.

Davidos skrev :

Det är här det tar stopp, jag vet att man kan stoppa in värden i den funktionen för att få fram y-värden. 

Men vet inte vart jag skall börja med ax^2+bx+c. Helt förträngt det.

Symmetrilinjen ligger vid $x=\frac{b}{2a}$, vilket direkt ger dig att $b=0$.

Din andragradskurva lyder då $y=ax^2+c$.

Med dina kända punkter på kurvan (3,75 : 0) och (7,5 : 10) så gäller det alltså att

$0=a\cdot 3,75^2+c$

$10=a\cdot 7,5^2+c$

Lös detta ekvationssystem för att bestämma a och c.

Sitter och kikar på ax^2+bx+c, tydligt att jag lär repetera detta lite. Men termen c, vad jag kan läsa av olika typer av andragradsekvationer är det var den korsar y axeln. Denna korsar ju i 0, så jag får det ju till att c ska va noll och inte b.

Om du ritar ut "hela" andragradskurvan ser du att den hamnar en bra bit under 0 när x = 0. Nu är ju skålen platt mellan -3,75 och 3,75, men andragradskurvan skulle fortsätta neråt i det intervallet.

Det är möjligt ja. Men variabeln b, vad bestämmer den?

Var symmetrilinjen finns. 

Grafen till $y=ax^2+bx+c$ kallas för en parabel.

Parabelns form och placering beror på konstanterna a, b och c på följande sätt:

• Om a > 0 så ser grafen ut som en "glad mun" (minnesregel "positiv = glad").
• Om a < 0 så ser grafen ut som en "ledsen mun" (minnesregel "negativ = ledsen").
• Om a är stort till beloppet så ser grafen ut som en skål (eller uppochnervänd skål) med väldigt branta väggar.
• Om a är litet till beloppet så ser grafen ut som en skål (eller uppochnervänd skål) med väldigt flacka väggar.
• Symmetrilinjen ligger vid $x=-\frac{b}{2a}$, så a och b bestämmer tillsammans var i horisontell led (sidled) som grafen ligger.
• Grafen skär y-axeln i $y=\frac{c}{a}$, så a och c bestämmer tillsammans var i vertikal led (höjdled) som grafen ligger.

Som om mitt huvud säger nej till det här, fantastiskt också att man läst igenom hela matte 4 boken och krånglar med en andragradsekvation.

 Men ekvationen 

0=a⋅3,752+c0=a·3,752+c

10=a⋅7,52+c10=a·7,52+c

Löser ut c i första ekvationen, stoppar in det i andra ekvationen. Men får ju inget som efterliknar att jag har en platt botten i grafen när man plottar på räknaren.

För jag ska väl kunna plotta grafen och få en platt yta som skålen?

Davidos skrev :

Som om mitt huvud säger nej till det här, fantastiskt också att man läst igenom hela matte 4 boken och krånglar med en andragradsekvation.

 Men ekvationen 

0=a⋅3,752+c0=a·3,752+c

10=a⋅7,52+c10=a·7,52+c

Löser ut c i första ekvationen, stoppar in det i andra ekvationen. Men får ju inget som efterliknar att jag har en platt botten i grafen när man plottar på räknaren.

För jag ska väl kunna plotta grafen och få en platt yta som skålen?

Nej sambandet gäller endast för $y\geq 0$.

Rita kurvan och tänk dig att x-axeln utgör skålens botten. Ser det bättre ut då?

Ja jo, ett steg närmre då. Såg att jag gjort lite kaos i uträkningen. Men det verkar stämma bra nu.

Återkommer om det uppstår mer problem.

Får tacka för hjälpen så här långt :)

Så jag satt och kika lite mer på  uppgiften nu. Värdena stämmer bra på bredden i botten. Alltså kurvan korsar på 3,75 och -3,75.

Det som inte stämmer är ju att när y=10 så korsar kurvan på -5,37 och 5,37 i x-led. 

Fått funktionen 0,652x^2-8,79

Davidos skrev :

Så jag satt och kika lite mer på  uppgiften nu. Värdena stämmer bra på bredden i botten. Alltså kurvan korsar på 3,75 och -3,75.

Det som inte stämmer är ju att när y=10 så korsar kurvan på -5,37 och 5,37 i x-led. 

Fått funktionen 0,652x^2-8,79

Visa hur du har kommit fram till den funktionen så kan vi hjälpa dig att hitta felet.

Löste de. Däremot problemet jag har nu, hur får jag fram arean ovanför kurvan med gränsområden på y=10 och x=-7,5 och x= 7,5

Det lyder väl som så att övre funktionen minus nedre funktionen, där övre är y=10 och en primitiv till detta blir bara 10x?

Räknaren räknar fram arean under kurvan genom graf funktionen. Sen kan man ju räkna integralen genom math funktionen, men är det den primitiva funktionen jag knappar in där eller andragradsfunktionen? 

Lite grötigt men kanske begripligt ändå?

Vilken andragradsfunktion kom du fram till?

Davidos skrev :

Löste de. Däremot problemet jag har nu, hur får jag fram arean ovanför kurvan med gränsområden på y=10 och x=-7,5 och x= 7,5

Det lyder väl som så att övre funktionen minus nedre funktionen, där övre är y=10 och en primitiv till detta blir bara 10x?

Räknaren räknar fram arean under kurvan genom graf funktionen. Sen kan man ju räkna integralen genom math funktionen, men är det den primitiva funktionen jag knappar in där eller andragradsfunktionen? 

Lite grötigt men kanske begripligt ändå?

Nej du ska använda skivmetoden.

Dela in rotationskroppen, dvs skålens volym, i jättemånga horisontella cirkulära skivor, var och en med en tjocklek dy.

Alla skivor har y-axeln som centrum och en radie r som beror av höjden y ovanför skålens botten.

Varje skiva har en yta som är $\pi r^2$ och med tjocklek dy så har varje skiva en volym som är area * tjocklek, dvs $\pi r^2 dy$.

Det är volymsbidraget från dessa skivor du ska integrera, från skålens botten (y = 0) till skålens rand (y = 10).

Nu gäller det bara för dig att komma på hur radien i kvadrat beror på y. Den kopplingen får du från din andragradsfunktion och din figur.

För du har väl ritat en figur?

Jag fick  0,237x^2-3,333

Okej radien beror ju på y, ju högre man går i y led desto större r. Ska kika på de nu igen, får se ifall man kommer någonvart.

Davidos skrev :

Jag fick  0,237x^2-3,333

 

Okej radien beror ju på y, ju högre man går i y led desto större r. Ska kika på de nu igen, får se ifall man kommer någonvart.

Det ser bra ut.

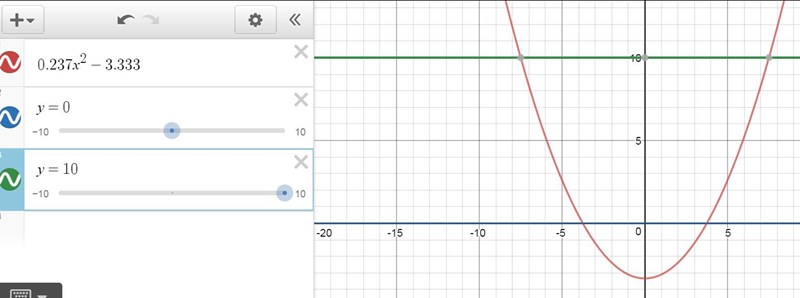
Så om man går tillväga som så att v=pi*r^2*dy

Där r är radien som kan bytas ut till x som då ger mig 

V= pi*x^2*dy

X^2 kan lösas ut från 0,237x^2-3,333 = y -->

0,237x^2 = y+3,333  -->

x^2 = (y+3,333)/0,237 -->

V = pi * ((y+3,333)/0,237) ^2 * dy

Detta som skall integreras?

Davidos skrev :

Så om man går tillväga som så att v=pi*r^2*dy

Där r är radien som kan bytas ut till x som då ger mig 

V= pi*x^2*dy

X^2 kan lösas ut från 0,237x^2-3,333 = y -->

0,237x^2 = y+3,333  -->

x^2 = (y+3,333)/0,237 -->

V = pi * ((y+3,333)/0,237) ^2 * dy

Detta som skall integreras?

Det ser jättebra ut. Integrera det uttrycket från y = 0 till y = 10 så får du fram skålens volym.

Det enda jag vill ändra på är att du kallar uttrycket för dV istället för V.

okej så nu när jag satt mig ner och skulle göra klart uppgiften så kommer jag ingenvart.

V = pi * ((y+3,333)/0,237) ^2

(y/0,237)^2 + (3,333/0,237)^2 

((y+3,333)/0,237) * ((y+3,333)/0,237) = (y^2 +6,666y + 11,109)/0,056

När jag fortsätter på detta blir det väldigt skumt. 

'

Davidos skrev :

okej så nu när jag satt mig ner och skulle göra klart uppgiften så kommer jag ingenvart.

V = pi * ((y+3,333)/0,237) ^2

Detta stämmer fast det saknas ett dy.

(y/0,237)^2 + (3,333/0,237)^2 

Här förstår jag inte vad du har gjort och du har tappat bort faktorn pi (och dy).

((y+3,333)/0,237) * ((y+3,333)/0,237) = (y^2 +6,666y + 11,109)/0,056

Ja bu stämmer det igen fast du har tappat bort både pi och dy.

När jag fortsätter på detta blir det väldigt skumt. 

'

Jag föreslår att du inför bokstäver att räkna med istället för siffror så blir det mindre rörigt.

Sätt dV = pi*((y + a)/b)^2 dy, där a = 3,333 och b = 0,237.

dV = pi*((y^2 +2ay + a^2)/b^2) dy

dV = pi*(y^2/b^2 +2ay/b^2 + a^2/b^2) dy

Detta ska nu integreras från y = 0 till y = 10.

En primitiv funktion är

pi*(y^3/(3b^2) + (2ay^2)/(2b^2) + (a^2y)/b^2).

Integralens värde är alltså

V = pi*(10^3/(3b^2) + (2a*10^2)/(2b^2) + (a^2*10)/b^2).

Sätt in värden på a och b och beräkna uttryckets värde.

Att jag inte stoppade in pi är väl för att den kan man ha utanför när man gör en primitiv funktion?

Varvid sedan Multiplicerar man in den, dy skriver jag typ aldrig ut. Kanske borde göra de.

Så långt har jag kommit och när jag beräknar detta.

(10^3) / (3*0,056) + (6,666*10^2) / (2 * 0,056) + (11,109 * 10) / ( 0 ,056)

18,667 + 18,666 + 1983,75 = 2021,083. multiplicera detta med pi blir det ju skumt.

Du bör alltid ha med dy (eller motsvarande) när du skriver en integral. Ibland integrerar man m a p x, ibland m a p y , ibland m a p t- det är en onödig risk man tar när men inte skriver ut sin integrationsvariabel.

Varför skulle det vara skumt att multiplicera ett numeriskt värde med pi?

Har du t ex beräknat hur stor volym en cylindrisk skål med diametern 15 cm och höjden 10 cm skulle ha, så att du vet om du får ett rimligt värde?

m a p?

Joo för att volymen stämmer inte, tog ju måtten från en skål hemma hos föräldrarna när jag va där. Skålen skall rymma 1 liter, därför jag tycker det är skumt?

Hej Davidos.

Jag ber om ursäkt, jag missade att du råkade göra en kvadrering för mycket i ett tidigare inlägg. Se här:

-----------------------------------------

Så här ska det vara:

Skålens form ges av sambandet $y=0.237x^2-3.333$, dvs $x^2=\frac{y+3.333}{0.237}$.

Eftersom en skiva har volymen $dV={\mathrm{\pi r}}^2 \mathrm{dy}$ och $r^2=x^2$ så får vi att en skiva har volymen

$dV={\mathrm{\pi x}}^2\mathrm{dy}=\mathrm{\pi }\left(\frac{\mathrm{y}+3.333}{0.237}\right)\mathrm{dy}=\frac{\mathrm{\pi }}{0.237}\left(y+3.333\right)dy$.

För att få med bidraget från alla skivor så integrerar vi detta från $y=0$ till $y=10$:

$V={\int }_0^{10}\frac{\mathrm{\pi }}{0.237}(y+3.333)dy=\frac{\mathrm{\pi }}{0.237}{\int }_0^{10}\left(y+3.333\right)dy$

En primitiv funktionen till $\left(y+3.333\right)$ är $\left(\frac{y^2}{2}+3.333y\right)$ och vi får därför integralens värde att bli

$V=\frac{\mathrm{\pi }}{0.237}\left(\left(\frac{{10}^2}{2}+3.333·10\right)-\left(\frac{0^2}{2}+3.333·0\right)\right)=\frac{\mathrm{\pi }}{0.237}·83.33\approx 1105$

Den beräknade volymen är alltså ungefär lika med 1105 $c{m}^3$, vilket är ungefär lika med 1,1 $d{m}^3$, dvs ungefär 1,1 liter.

Jaaa det har jag ja. Men när du integrerar funktionen.  π(y+3.3333/0,237)dy

Det enda jag inte är med på är varför 0,237 inte skall integreras ?

Davidos skrev :

Jaaa det har jag ja. Men när du integrerar funktionen.  π(y+3.3333/0,237)dy

Det enda jag inte är med på är varför 0,237 inte skall integreras ?

Det saknas en parentes i täljaren i ditt uttryck.

Det ska stå π((y+3.3333)/0,237) dy

Detta är lika med (π/0.237)*(y+3.3333) dy

(π/0.237) är alltså en faktor framför integranden.

-------

På samma sätt som den primitiva funktionen av 7*y är 7*(y^2/2) + C så är den primitiva funktionen av (π/0.237)*y lika med (π/0.237)*(y^2/2) + C.

Så är även den primiva funktionen av (π/0.237)*(y+3.3333) lika med (π/0.237)*(y^2/2+3.3333y) + C.