Vad är det du behöver hjälp med? Att skriva integralen? Att hitta integrationsgränserna? Att hitta en primitiv funktion? Nånting annat?
Smaragdalena skrev:Vad är det du behöver hjälp med? Att skriva integralen? Att hitta integrationsgränserna? Att hitta en primitiv funktion? Nånting annat?
Hitta kntegralgränserna vore toppen att få hjälp med!
hur är det med integralen? Använder jag mig bara av den som står i uppgiften och gör en primitiv funktion av den som vanligt?
Vilken är överfunktionen? Vilken är underfunktionen?
Smaragdalena skrev:Vilken är överfunktionen? Vilken är underfunktionen?
Hur kan jag ta reda på detta?
Titta på bilden.
Smaragdalena skrev:Titta på bilden.
Antar att det är underfunktionen jag är ute efter. Aldrig tagit reda på en sådan tidigare, tanken jag har är att det möjligtvis ska va minus y=-sin(2x+pi/2)
Nej, den funktionen är inte utritad i bilden. Funktionen i överkanten av det streckade området är y = 0. Detta är överfunktionen. Vilken är underfunktionen? (Läs i texten ovanför bilden.)
Smaragdalena skrev:Nej, den funktionen är inte utritad i bilden. Funktionen i överkanten av det streckade området är y = 0. Detta är överfunktionen. Vilken är underfunktionen? (Läs i texten ovanför bilden.)
Okej! Om funktionen i överkanten är y=0 så är underkanten möjligtvis y=-1 Då den vänder i det y-värdet?
Smaragdalena skrev:Nej, den funktionen är inte utritad i bilden. Funktionen i överkanten av det streckade området är y = 0. Detta är överfunktionen. Vilken är underfunktionen? (Läs i texten ovanför bilden.)
Okej! Om överkanten är y= 0 borde underkanten möjligtvis vara y=-1 ? Om jag söker efter y-värdet där funktionen vänder
Nej, det skall vara funktionen som är nederkanten av det streckade området. Det är en sinusfunktion, som beskrivs i texten.
Smaragdalena skrev:Nej, det skall vara funktionen som är nederkanten av det streckade området. Det är en sinusfunktion, som beskrivs i texten.
Sinusfunktionen som är i texten är y=sin(2x+pi/2) som inte var den funktionen jag sökte?
Jo, det är den underfunktionen du söker - den är i underkanten av det streckade området.
Smaragdalena skrev:Jo, det är den underfunktionen du söker - den är i underkanten av det streckade området.
Okej! Så nu har jag 2 funktioner, en över och en under. Nu måste jag hitta integralgränserna?
Ja. Titta på bilden! I den här uppgiften är det OK att läsa av gränserna i bilden, oftast behöver man ta fram dem algebraiskt.
Smaragdalena skrev:Ja. Titta på bilden! I den här uppgiften är det OK att läsa av gränserna i bilden, oftast behöver man ta fram dem algebraiskt.
Okej! Vilken av funktionerna är det jag ska göra en primitiv funktion på? Eftersom att jag har både en övre och undre?
Har du hittat gränserna?
Övre funktionen minus undre funktionen.
Smaragdalena skrev:Har du hittat gränserna?
Övre funktionen minus undre funktionen.
Väldigt osäker men möjligtvis x=0,25pi och 0,75pi. Ser ut som att det ökar med 0,25pi per ruta.
Det stämmer. Då vet du gränserna. Vilken är integranden, d v s funktionen som skall integreras?
Smaragdalena skrev:Det stämmer. Då vet du gränserna. Vilken är integranden, d v s funktionen som skall integreras?
eftersom att den övre gränsen är y=0 och inte går att göra så mycket med ska jag möjligtvis använda mig av den undre?
Integranden skall vara överfunktion minus underfunktion. Vad blir det?
Smaragdalena skrev:Integranden skall vara överfunktion minus underfunktion. Vad blir det?
0-sin(2x+pi/2) = -sin(2x+pi/2)
Ja. Vet du hur du skall ta reda på den primitiva funktionen?
Smaragdalena skrev:Ja. Vet du hur du skall ta reda på den primitiva funktionen?
Det vet jag! Tack så jättemycket för all hjälp!

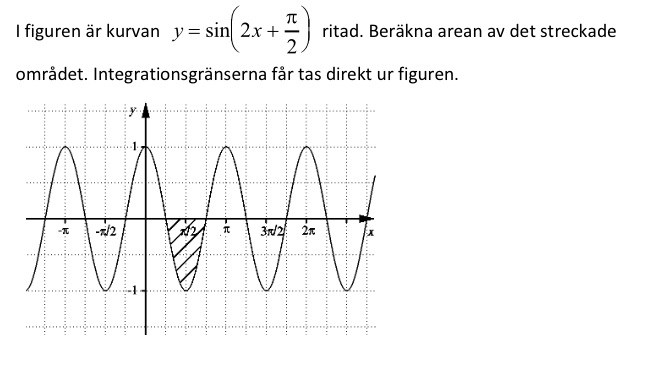 Skulle behöva lite hjälp med uppgiften ovan!
Skulle behöva lite hjälp med uppgiften ovan!
