Konvertera Explicit Euler lösning till Implicit Euler (med fixpunktsmetoden)
Jag har "en" uppgift som ser ut såhär:



Jag har redan löst uppgift A och B (men hade med dem för kontext) och nu har jag fastnat på uppgift G. Jag vet inte riktigt var jag ska börja.
MATLAB koden för uppgift B (fall 2, acceleration) ser ut såhär (funktionen "Func" är funktionen från uppgift A):
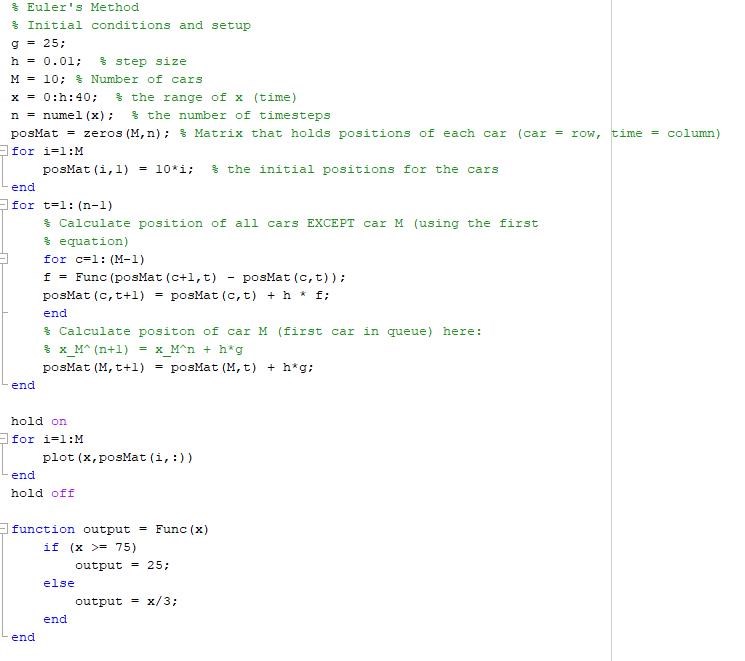
Det ända som jag gjort i Uppgift G är att jag skrivit en funktion för fixpunktsmetoden:
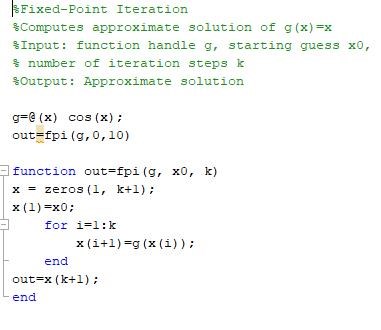
Borde jag modifiera koden i Uppgift B eller är det en bättre idé att skriva koden för bakåt Euler från scratch? Har ni några tips på hur jag kan modifiera koden i Uppgift B för att uppfylla kraven i Uppgift G? Jag vet ungefär hur bakåt Euler fungerar men har lite svårt med integrera detta kodmässigt (modifiera koden i B). MATLAB är nytt för mig.
Förlåt för den långa texten.
Tack!
Hej!
Du har alltså differentialekvationen för ledarbilen
och differentialekvationerna för de stycken efterföljande bilarna
.
Jag skriver bara om ledarbilen och överlåter till dig att tillämpa det jag skriver på de efterföljande bilarna.
Eulers bakåtmetod tillämpad på ledarbilen ger talföljden där
och .
Givet ska man alltså lösa den icke-linjära ekvationen
för att finna .
Definiera därför funktionen så att du ska lösa ekvationen
;
som du ser är en fixpunkt till funktionen . Skapa en fixpunktsiteration
och använd förslagsvis startvärdet Kontrollera att funktionen verkligen är en kontraktionsavbildning så att du är försäkrad om att fixpunktsiterationen konvergerar; du kanske även måste formulera om fixpunktsiterationen för att snabba på konvergenshastigheten om talföljden verkar konvergera alltför långsamt (snabb konvergens är viktig eftersom du måste köra om fixpunktsiterationen för att finna ledarbilens nästa position ).
En kommentar om din fixpunktskod:
Det är onödigt att spara successiva iterationer i en vektor (x); jag föreslår istället att du har ett enda tal som du uppdaterar vid varje iteration ända tills önskad noggrannhet nåtts och att du även håller koll på antalet iterationer, så att koden stoppar om den har varit igång för länge utan att önskad noggrannhet erhållits.
Förslagsvis kan koden ge output "Konvergens har ej nåtts efter N iterationer", där N är specificerat av användaren i förväg (exempelvis N = 100) om detta inträffar; i annat fall blir output en approximation till den sökta fixpunkten. (Man kan även tänka sig att output inkluderar texten "Konvergens har nåtts efter k iterationer" där k är index för den iteration efter vilken önskad noggrannhet uppnåtts.
Input till proceduren FixPunktIter är funktionen g, startvärde x0, önskad noggrannhet och Maximalt antal tillåtna iterationer (N).
Albiki skrev:Hej!
Du har alltså differentialekvationen för ledarbilen
och differentialekvationerna för de stycken efterföljande bilarna
.
Jag skriver bara om ledarbilen och överlåter till dig att tillämpa det jag skriver på de efterföljande bilarna.
Eulers bakåtmetod tillämpad på ledarbilen ger talföljden där
och .
Givet ska man alltså lösa den icke-linjära ekvationen
för att finna .
Definiera därför funktionen så att du ska lösa ekvationen
;
som du ser är en fixpunkt till funktionen . Skapa en fixpunktsiteration
och använd förslagsvis startvärdet Kontrollera att funktionen verkligen är en kontraktionsavbildning så att du är försäkrad om att fixpunktsiterationen konvergerar; du kanske även måste formulera om fixpunktsiterationen för att snabba på konvergenshastigheten om talföljden verkar konvergera alltför långsamt (snabb konvergens är viktig eftersom du måste köra om fixpunktsiterationen för att finna ledarbilens nästa position ).
Tja, vi har lite problem med att förstå hur vi ska översätta detta till kod. Skulle du kunna ge något exempel?
Detta har vi förstått:
Vi vill ha en approximativ position för varje bil i ett visst ögonblick så y=G(y) där tex för bil M G(u)= x(t,M)+h*g. Alltså söker vi ett u (dvs en position) så att u=G(u). Det löser vi genom att loopa igenom en FPI med y_i+1=G(y_i) med ett begynnelsevillkor y_0= x(1,M)=750. Då blir exempelvis y_2=G(y_1)= 750 +h*5.

