Kulans laddning
Alltså, jag tror att det är två formler jag ska kombinera. Den ena är men andra vet inte...

Fick inte till det. och Det ger: fel svar.
Rätt svar är
Du ska nog använda vinkeln också.
Som vanligt: Har du ritat?
Jag har ritat men jag vet inte hur jag ska använda vinkeln i beräkningarna.
Visa bilden. Har du satt ut alla krafter?
Jag fick ett värde på , vilket stämmer ganska bra med facit. Men hur ska man resonera kring om det är eller i beräkningarna?
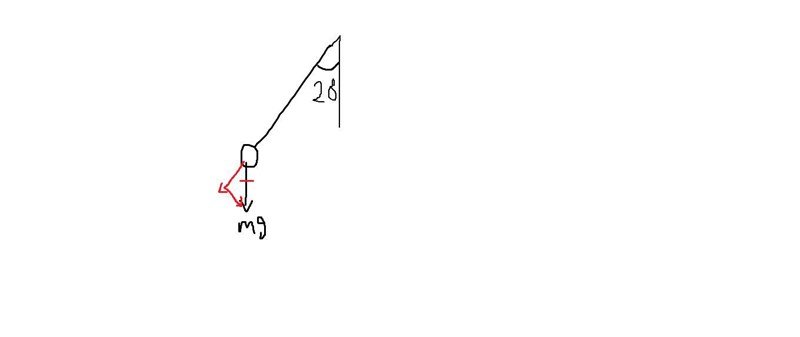
mg är rätt, men vad är de andra för något?
Komponenterna.
OK. Om det bara ser ut så så skulle kulan falla neråt. Var är den elektriska kraften?
Elektriska kraften pekar åt vänster.
Ta med den i bilden.
Laguna skrev:Ta med den i bilden.
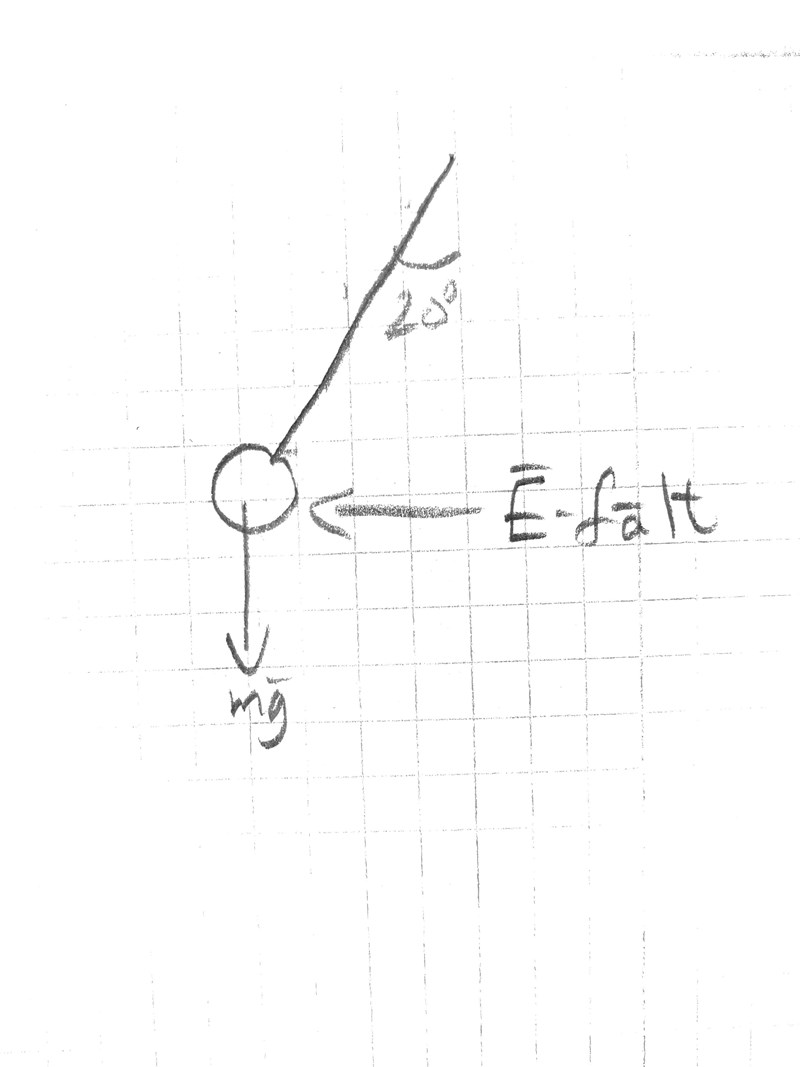
Då har du (om du flyttar om vektorpilarna lite) en rätvinklig triangel med kateterna mg respektive Eq. Vilken trigonometrisk funktion kan du ha nytta av i det här fallet?
Det blir tangens. Men jag förstår forfarande inte varför.
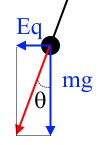 Den resulterande kraften (den röda vektorn) ska enligt kraftjämvikt uppfylla
Den resulterande kraften (den röda vektorn) ska enligt kraftjämvikt uppfylla
Lös vi ut q från ekvationerna får vi
Den tredje kraften som verkar på kulan är spännkraften i snöret. Du kan ställa upp samband mellan de tre krafterna med hjälp av trigonometri.





