Linjär avbildning rotation, spegling

Jag ska ta fram standardmatriserna till A och B och undrar hur jag ska göra det. Standardmatrisen ges av T(1,0) och T(0,1) och för A då det är spegling ska man ta formeln för reflektion dvs T(1,0)= 2projv(1,0)-(1,0) och sen T(0,1)= 2projv(0,1)-(0,1) eller finns det nåt annat sätt att lösa uppgiften på? Om man gör man det då får man fram att
A= -2 -1
1 -1
Kan du visa mer av hur du har gjort? Jag ritade upp dina startpunkter och speglade punkter och det ser inte helt speglat ut..
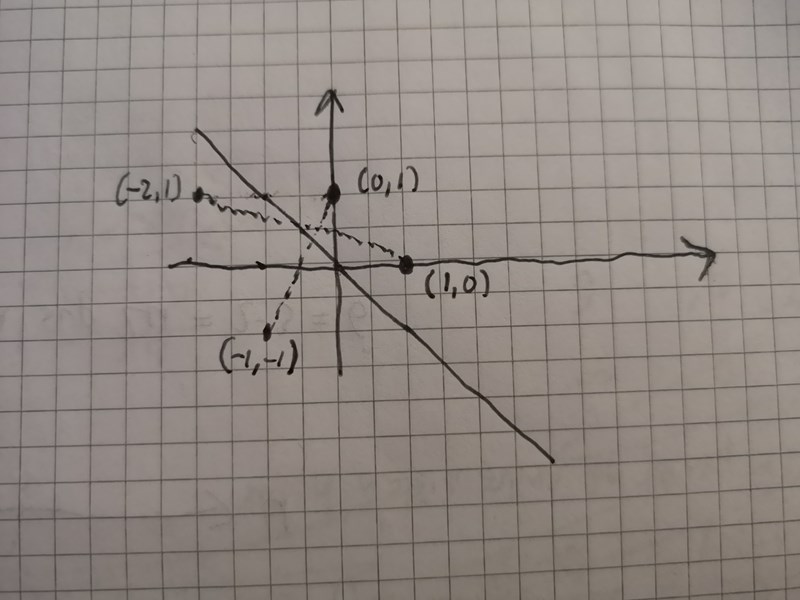
Du har använt rätt formler men du måste gjort något räknefel på vägen. Visa hur du räknar så kan vi kanske hitta felet.
Ett tips:
Speglingen är en så kallad involution, dvs om du speglar en vektor för att sedan spegla den speglade vektorn så får du tillbaka den ursprungliga vektorn. Det betyder att en spegling är sin egen invers.
Således måste matrisen A uppfylla att A2 = I. Så du har ett sätt att testa att resultatet är rimligt.
Notera att vi kan erhålla matrisen för speglingen på ett enkelt sätt.
.
S() = , vilket innebär att
A = .
A2 = = . Check!
Tack! Aa tror jag har räknat fel ska räkna om.


