Logaritmer, exponentialfunktioner.
Jag är medveten om att man använder formeln
Så min tanke var att jag kunde använda en punkt. så jag tog (0,3).
3=C*a^0
Då tänkte jag att någonting upphöjt i 0 = 1
så då skrev jag om det
3=C*1
3=C
och då få uttrycket .
Svaret är f(x) = .
Om någon kan berätta vart jag gick fel uppskattar jag det. Mvh Pepsi
Var fick du ettan från i ? Du fick c=3, det är rätt, men hur vet du att a=1?
(Förresten vill jag bara säga att y=cax inte är en formel, det kallas för ett uttryck för en generell exponentialfunktion. Och om du någonsin träffar på en exponentialfunktion där a=1 så är något vääääldigt fel)
Du har gjort rätt, men du har bara fått fram att C = 3. Du behöver nu använda den andra punkten för att hitta a också. Du vet att , använd nu den andra punkten du fått för att hitta a. :)
eftersom att jag tog punkten (0,3) så betyder detta att x = 0.
a^0=1
Eftersom att exempelvis 100000^0=1 eller är jag helt ute och cyklar?
Nja, x är en variabel. x är lika med noll på ett specifikt ställe bara. (vadsomhelst)^0=1 är sant, ja. Men a är inte lika med 1
y=3a^x
/ 3
Sedan använde jag mig av en potenslag och det här blev bara konstigt. gjorde jag nå fel här eller?
a^-1 Krånglar till lite här. Jag väll korsmultiplicera men hur fungerar det med a^-1
pepsi1968 skrev:y=3a^x
/ 3
Sedan använde jag mig av en potenslag och det här blev bara konstigt. gjorde jag nå fel här eller?
a^-1 Krånglar till lite här. Jag väl korsmultiplicera men hur fungerar det med a^-1
Du har gjort lite fel:
då blir det rätt! :)
Hej!
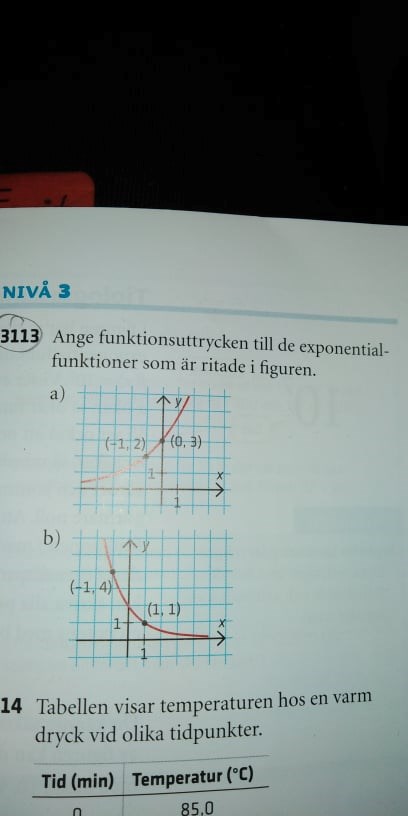
Uppgift 3113: I båda fallen är det lämpligt att använda sambandet
Man ser att alla y-värden är positiva så konstanten .
- I uppgift a) växer när ökar, vilket indikerar att konstanten ; notera den strikta olikheten.
- I uppgift b) avtar när ökar, vilket indikerar att konstanten a är sådan att .
Notera att om konstanten hade varit exakt lika med så hade grafen varit en horisontell linje för alla .
För att bestämma konstanternas exakta värden kan du använda de två givna punkterna i varje figur.
Uppgift a) Punkten säger att
Punkten säger att och tillsammans med kunskapen att får man konstanten via sambandet . Notera att som tidigare nämnts.
Uppgift b) Punkten säger att
Punkten säger att och tillsammans med kunskapen att och är kopplade via sambandet får man konstanten via sambandet
notera att inte är aktuellt eftersom det skulle göra funktionsvärden till komplexa tal.
Albiki skrev:Hej!
Uppgift 3113: I båda fallen är det lämpligt att använda sambandet
Man ser att alla y-värden är positiva så konstanten .
- I uppgift a) växer när ökar, vilket indikerar att konstanten ; notera den strikta olikheten.
- I uppgift b) avtar när ökar, vilket indikerar att konstanten a är sådan att .
Notera att om konstanten hade varit exakt lika med så hade grafen varit en horisontell linje för alla .
För att bestämma konstanternas exakta värden kan du använda de två givna punkterna i varje figur.
Uppgift a) Punkten säger att
Punkten säger att och tillsammans med kunskapen att får man konstanten via sambandet . Notera att som tidigare nämnts.
Uppgift b) Punkten säger att
Punkten säger att och tillsammans med kunskapen att och är kopplade via sambandet får man konstanten via sambandet
notera att inte är aktuellt eftersom det skulle göra funktionsvärden till komplexa tal.
Jag förstod inte riktigt vaddu gjorde i dem två sista stegen. Eller hur man kan använda de två punkterna för att lösa frågan. Jag tog ny punkt på b) (0,2) Kan man lösa utan?
Läroboken är så snäll att den bjuser dig på två lämpliga punkter att sätta in, (-1,4) och (1,1) i b-uppgiften. Tacka oh ta emot! Du kan inte vara alldeles säker på att punkten (0,2) verkligen ligger på kurvan (även om det ser ut som om den gör det).
Du vet att y=Cax och att C=a-1. Sätt in detta värde på C samt x=-1 och y=4 i formeln y=Cax, så får du fram ett värde på a.
Det visar sig att punkten (0,2) också ligger på linjen, så det fungerar lika bra med den. Då skulle du ha fått ekvationen 2=a-1a0, vilket ger att a-1=2 och a=½.
Smaragdalena skrev:Läroboken är så snäll att den bjuser dig på två lämpliga punkter att sätta in, (-1,4) och (1,1) i b-uppgiften. Tacka oh ta emot! Du kan inte vara alldeles säker på att punkten (0,2) verkligen ligger på kurvan (även om det ser ut som om den gör det).
Du vet att y=Cax och att C=a-1. Sätt in detta värde på C samt x=-1 och y=4 i formeln y=Cax, så får du fram ett värde på a.
Det visar sig att punkten (0,2) också ligger på linjen, så det fungerar lika bra med den. Då skulle du ha fått ekvationen 2=a-1a0, vilket ger att a-1=2 och a=½.
Okej, men. Du säger y=ca^x, hur kan du då säga att C=a^-1. vad händer med y? ingen av punkterna visar att y=0?. Och som han tog upp " y(1)=1⇔1=Ca1⇔C=a−1." vart går ettan? saker försviner känns de som här
Har du glömt att vadsomhelst0=1?





