4
svar
79
visningar
Lös följande komplexa ekvaioner
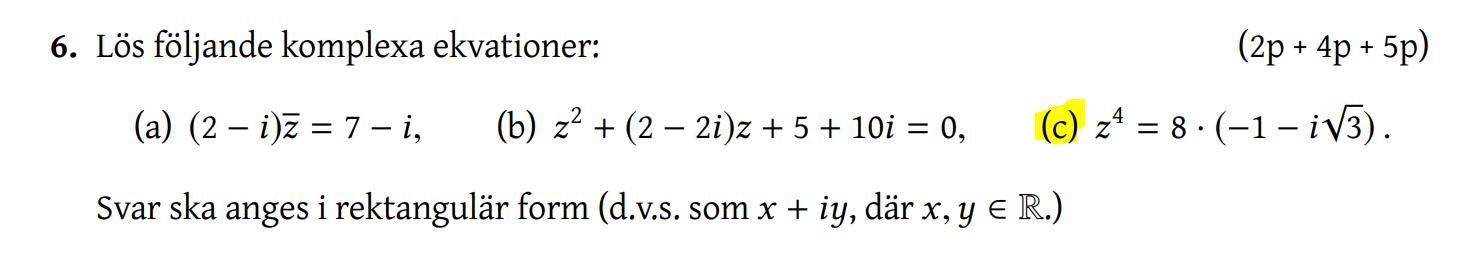
Facit:
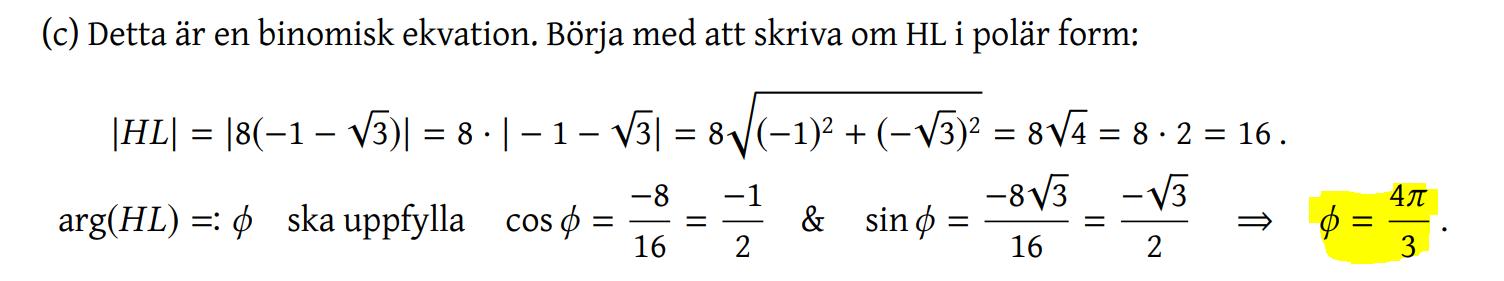
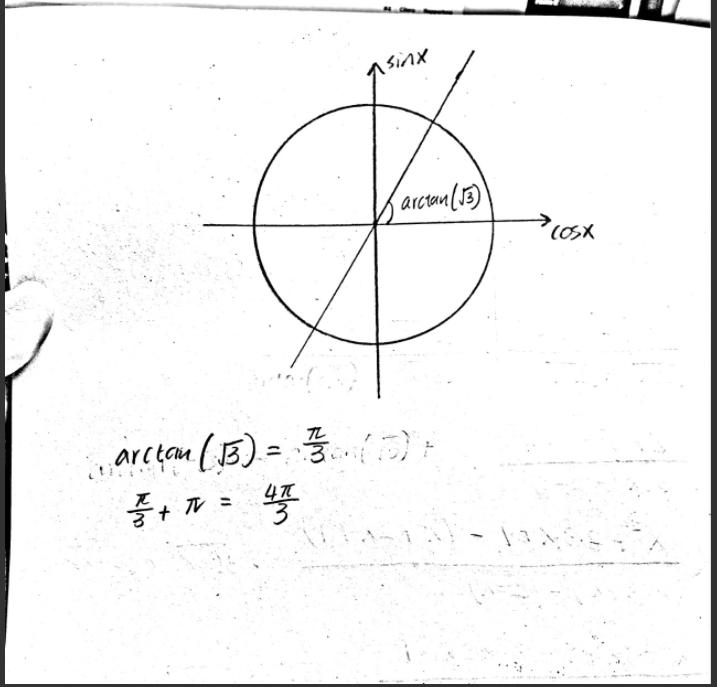
Varför fick inte samma vinkeln som i facit?
Eftersom både real och imagimärdelarna är negativa måste vi vara i tredje kvadranten där vinkel är mellan pi och 3pi/2
Arctan funkar bara för att få fram en vinkel på högra delen av enhetscirkeln. Rita istället.
Tangensfunktionen har perioden pi, från -pi/2 till pi/2, sen upprepar den sig.
Därför måste man själv hålla reda på i vilken halva av det komplexa talplanet som z befinner sig i.
Som i de flesta fall: Rita!
Båda Rea och Im delen är negativa således att vinkeln måste befinner sig i den tredje kvadranten.