Lyckades lösa en knepig en, försök du med! (Enklare variant!)

Här kommer en variant på lösning:

tomast80 skrev:

Här kommer en variant på lösning:

 WOW! Imponerande! Väldigt klokt, så tänkte inte jag. 


EDIT: mini ledtråd. 
Jag tror att de flesta känner till en annan metod där man kan förlänga bråket med något för att kunna lösa uppgiften, om det dock finns någon som vet hur man kan lösa den med en tredje metod så får ni mer än gärna visa det. 

tomasts lösning är definitivt finurlig, men då måste jag vara jobbig och fråga:

Om vi tillåts på förhand veta derivatan av uttryck som inte är $f(x)$, betyder då "med derivatans definition" bara att vi använder derivatans definition någonstans i uträkningen?

I så fall kan vi väl lika gärna bara modifiera tomasts lösning och göra så här:

$2f(x)f'(x)$ $=\dfrac{d}{dx}[x^2+1]$

$2f(x)f'(x)$ $=\dfrac{d}{dx}[x^2+1]+\dfrac{d}{dx}[0]$

$2f(x)f'(x)$ $=2x+\lim_{h\to0} \dfrac{0-0}{h}$

$2f(x)f'(x)=2x+0$

$f'(x)$ $=\dfrac{2x}{2f(x)}=\dfrac{x}{\sqrt{x^2+1}}$

Det var en relevant fråga.

Ett alternativ där man utgår från derivatas defintion torde dock vara att definiera:

$g(x) =x^2+1$

$h(x)=\sqrt{x}$

och bestämma derivatan genom att härleda kejderegeln utifrån derivatans definition:

$f'(x)=\frac{h(g(x+h))-h(g(x))}{h}$ och låta $h\to 0$.

tomast80 skrev:

Det var en relevant fråga.

Ett alternativ där man utgår från derivatas defintion torde dock vara att definiera:

$g(x) =x^2+1$

$h(x)=\sqrt{x}$

och bestämma derivatan genom att härleda kejderegeln utifrån derivatans definition:

$f'(x)=\frac{h(g(x+h))-h(g(x))}{h}$ och låta $h\to 0$.

 Ja, det är en variant. Dock går det faktiskt att lösa gränsvärdet för hela funktionen direkt genom att multiplicera med konjugatet:

Jag och Korra försökte i PM att slå våra kloka huvuden ihop för att se om det fanns några andra tillvägagångssätt än att använda detta konjugatknep, men vi hade svårt att komma på något. Jag var inne på det du talade om med kedjeregeln, men man behöver konjugatknepet för att lösa gränsvärdet för derivatan av $\sqrt{x}$, alltså är det i stort sett bara en tillkrånglad version av vad jag gjorde ovan.

Det här du kom på med implicit differentiering var dock något som jag inte hade tänkt på. Kanske går det att bevisa derivatan av $(f(x))^2$ med derivatans definition och på så sätt inte "fuska" med någon förhandskunskap?

Mycket snyggt! Bra idé, vad sägs om följande:

$\frac{d}{dx}\left(f\right(x){)}^2=$

$\underset{h\to 0}{\lim }\frac{\left(f\right(x+h){)}^2-(f\left(x\right){)}^2}{h}=$

$\underset{h\to 0}{\lim }\frac{\left(f\right(x+h)+f(x\left)\right)\left(f\right(x+h)-f(x\left)\right)}{h}=$

$\lim_{h\to 0}(f(x+h)+f(x))\cdot \frac{f(x+h)-f(x)}{h}=$

$2\cdot f(x)\cdot f'(x)$

Q.E.D.

Om någon såg 3blue1browns Calculus done right serie så fanns däri en hel del eleganta geometriska bevis för derivatorna av olika trigonometriska funktioner och man kan applicera några av de ideerna på denna funktion då det geometriskt motsvarar hypotenusan till en rätvinklig triangel med kateter 1 och x. 

Om x uttökas med en infinitessimal förlängning så ökar hypotenusan men kan anses vara effektivt parallell med ursprungshypotenusan. Från detta kan vi göra att litet likformighetrargument där triangeln som bildas i hörnet med proportion $\Delta y / \Delta x$ är likformig med triangeln som helhet vars proportioner är $x/\sqrt{x^2 +1}$

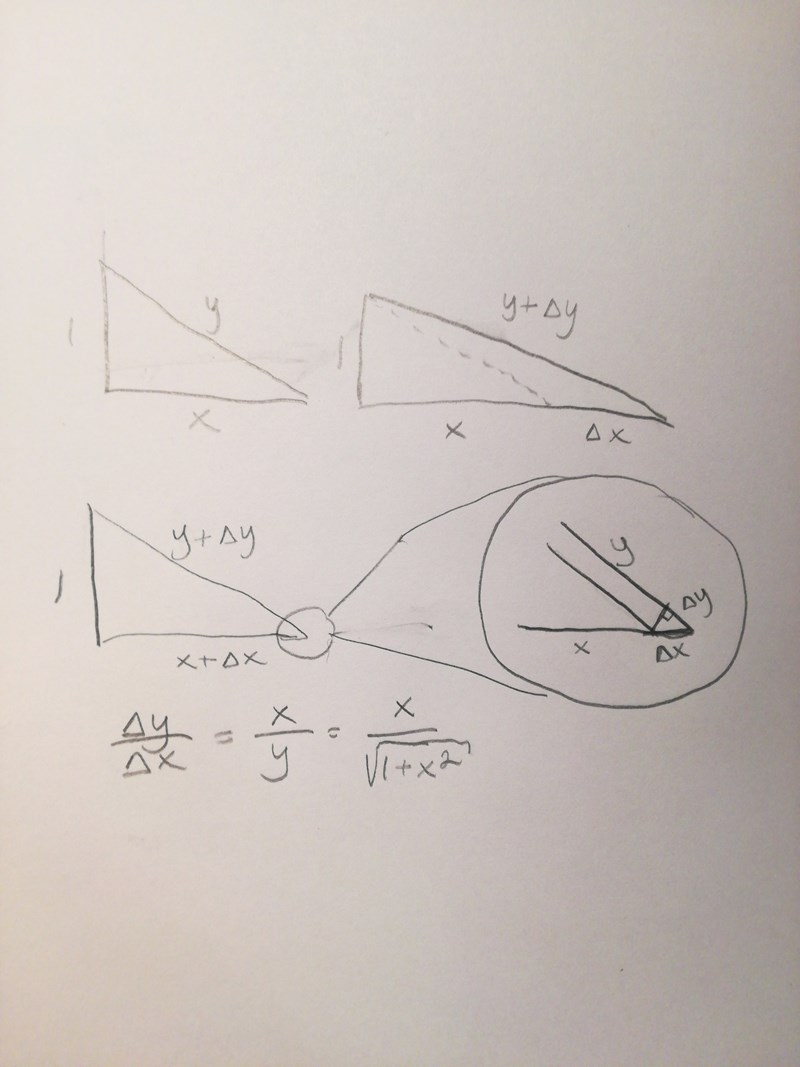
SeriousCephalopod skrev:

Om någon såg 3blue1browns Calculus done right serie så fanns däri en hel del eleganta geometriska bevis för derivatorna av olika trigonometriska funktioner och man kan applicera några av de ideerna på denna funktion då det geometriskt motsvarar hypotenusan till en rätvinklig triangel med kateter 1 och x. 

Om x uttökas med en infinitessimal förlängning så ökar hypotenusan men kan anses vara effektivt parallell med ursprungshypotenusan. Från detta kan vi göra att litet likformighetrargument där triangeln som bildas i hörnet med proportion $\Delta y / \Delta x$ är likformig med triangeln som helhet vars proportioner är $x/\sqrt{x^2 +1}$

Snyggt! Så kan man också göra!