Minsta kvadratanpassning

"Bestäm en matris A och en matris B så att lösningen X till ekvationssystemet $A^{T} A x = A^{T} B$ är en minsta kvadratanpassning av följande data på formen $\frac{{(x - a)}^{2}}{c^{2}} + \frac{{(y - b)}^{2}}{d^{2}} = 1$

(1,0),(2,1),(3,-1),(2,-1),(1,-3) "

Jag förstår inte hur jag ska kunna skriva om ekvationen. Facit säger att ekvationen måste linjäriseras med avseende på a,b,c och d, men vad innebär detta?

a, b, c och d är dina okända du söker att bestämma i detta system. Med andra ord vill du inte att din minstakvadratfunktion ska vara icke-linjär genom att det finns termer och uttryck så som $a^{2}$ eller $b c^{2} / d^{2}$ när du formulerar det överbestämda ekvationssystemet. Jag skulle göra så här:

$y = \frac{a^{2} d^{2} + b^{2} c^{2} - c^{2} d^{2}}{2 c^{2} b} + \frac{d^{2}}{2 c^{2} b} x^{2} - \frac{d^{2} a}{c^{2} b} x + \frac{y^{2}}{2 b}$

Med andra ord är det en ganska komplicerad affär i slutändan att bestämma de enskilda variablerna men vår minstakvadratfunktion blir enkel:

$f (x_{i}, {\tilde{x}}_{i}, {\tilde{y}}_{i}, u) = u_{1} + u_{2} {\tilde{x}}_{i} + u_{3} x_{i} + u_{4} {\tilde{y}}_{i}$

Där vi har att:

$\tilde{x} = x^{2} \tilde{y} = y^{2} u_{1} = \frac{a^{2} d^{2} + b^{2} c^{2} - c^{2} d^{2}}{2 c^{2} b} u_{2} = \frac{d^{2}}{2 c^{2} b} u_{3} = - \frac{d^{2} a}{c^{2} b} u_{4} = \frac{1}{2 b}$

Detta kan sedan formuleras i ett överbestämt ekvationssystem enligt:

$[\begin{matrix} 1 & {\tilde{x}}_{1} & x_{1} & {\tilde{y}}_{1} \\ 1 & {\tilde{x}}_{2} & x_{2} & {\tilde{y}}_{2} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ 1 & {\tilde{x}}_{5} & x_{5} & {\tilde{y}}_{5} \end{matrix}] [\begin{matrix} u_{1} \\ u_{2} \\ u_{3} \\ u_{4} \end{matrix}] = [\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{5} \end{matrix}]$

Om du mosar in detta i MATLAB eller liknande får du:

$u_{1} = - \frac{5}{3} u_{2} = - \frac{2}{3} u_{3} = \frac{7}{3} u_{4} = - \frac{1}{3}$

Detta i sin tur efter lite trixande ger värden på de konstanter vi vill ha:

$a = \frac{7}{4} b = - \frac{3}{2} c \approx 1.299 d \approx 1.837$

Vi kan nu kontrollera hur bra anpassningen är:

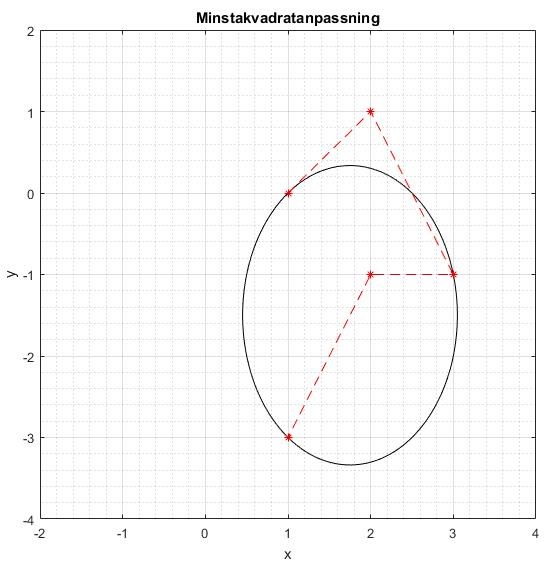
Detta är acceptabelt med tanke på antalet punkter. Residualens norm är $\sqrt{2}$ så det är ganska bra.

För att vidareutveckla så kan man testa en datamängd som är lite bättre. Vi tar en förbestämd ekvation för en ellips:

$\frac{{(x - 2)}^{2}}{2} + \frac{{(y - 1)}^{2}}{4} = 1$

Jag ritar denna i en graf och måttar en datamängd med ögonen på denna cirkel vilket ger följande tabell:

$\begin{matrix} x \\ y \end{matrix} \begin{matrix} 2 & 0.75 & 0.6 & 1 & 2 & 2.8 & 3.4 & 3.2 & 2.8 \\ - 1 & 0 & 1 & 2.4 & 3 & 2.5 & 1 & 0 & - 0.5 \end{matrix}$

Detta ger med metoden från tidigare inlägg följande anpassning:

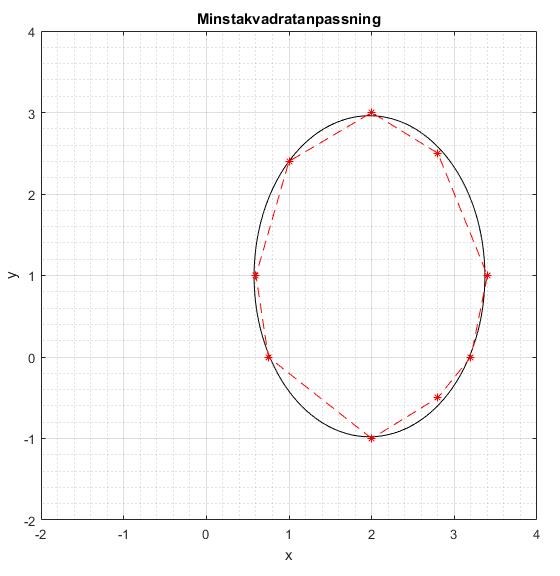
Synligt bättre anpassning denna gång och med en ungefärlig residualnorm på 0.25. Vi kan jämföra de bestämda konstanterna (blått) med de exakta värden från ellipsens ekvation (rött):

$\begin{matrix} a \approx 1.97 & a = 2 \\ b \approx 0.99 & b = 1 \\ c \approx 1.39 & c = \sqrt{2} \\ d \approx 1.97 & d = 2 \end{matrix}$

Svara Avbryt