Omfångsrika problem - Kontinuerlig ränta (Differentialekvationer)

Försöker lösa en uppgift som handlar om kontinuerlig ränta. Jag har gjort alla stegen i uppgiften fram till den som är "mer avancerat". Jag förstår inte hur detta ska bli en differentialekvation när vi visar att förändringen av tiden går mot noll.

Har börjat göra en del av uppgiften som jag bifogar nedan men jag vet inte om jag är på rätt spår...

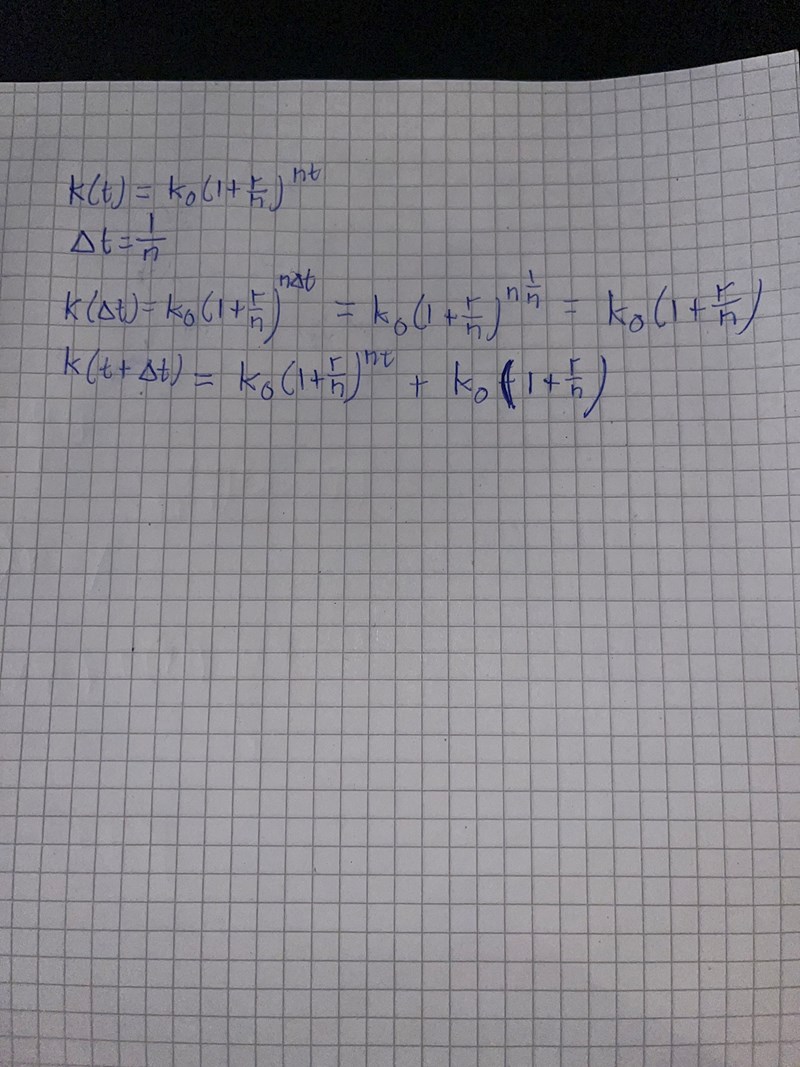
Lösningen är kanske enklare än du tror:

Definitionen av derivatan: $K' (t) = \lim_{∆ t \to 0} \frac{K (t + ∆ t) - K (t)}{∆ t}$

Det är därför att uppgiften säger att du ska uttrycka K(t+deltat) med K(t), r och deltat. Du behöver inte veta K(t).

Efter deltat tid (som är lika med 1/n) får du K(t)*r*deltat ränta.

Så

$K' (t) = \lim_{∆ t \to 0} \frac{K (t + ∆ t) - K (t)}{∆ t} = \lim_{∆ t \to 0} \frac{K (t) * (1 + r * ∆ t) - K (t)}{∆ t} = \lim_{∆ t \to 0} \frac{K (t) * r * ∆ t}{∆ t} = K (t) * r$

K'(t) = K(t)*r

Och den är differentialekvationen.

Svara Avbryt