Pendel med två olika massor
Frågan lyder:

Mitt försök:
Friläggningen:
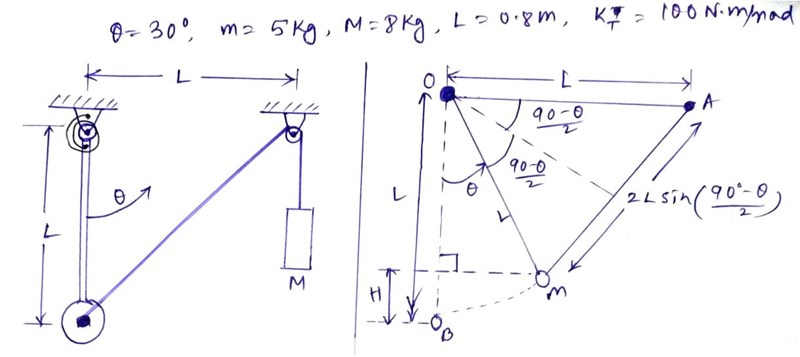
Jag vill lösa uppgiften med hjälp av vektorer.
Utöver detta tänker jag att man kan bilda vektoren och sedan defininera en rotationsmatris som roterar vektorn 30 grader moturs.
Problemet är bara att jag vill veta pendelns hastighet då .
Är inte säker på hur jag ska gå tillväga.
Jag ser ingen friläggning. En sådan ska innehålla krafter och moment. Tänk på att:
om .
Du ska använda energimetoder för att lösa a)-delen på denna uppgift, kolla exempelvis sample problem 3/18. Jag vet inte vad "Jag vill lösa uppgiften med hjälp av vektorer" betyder men när det kommer till b)-delen behöver du numeriska metoder för att få fram en lösning. Jag kan ge dig en bra start på a)-delen:
Den potentiella energin som lagras i fjädern är:
Du behöver nu formulera ett tvång mellan partikeln och massans rörelse. Du ser att hastighetsvektorn för partikeln har en komponent längs med snöret, denna är lika stor som hastighetsvektorn för massan. Du kan då formulera tvånget baserat på cosinus för vinkeln mellan dem. Se figur nedan över situationen och klarifiering:
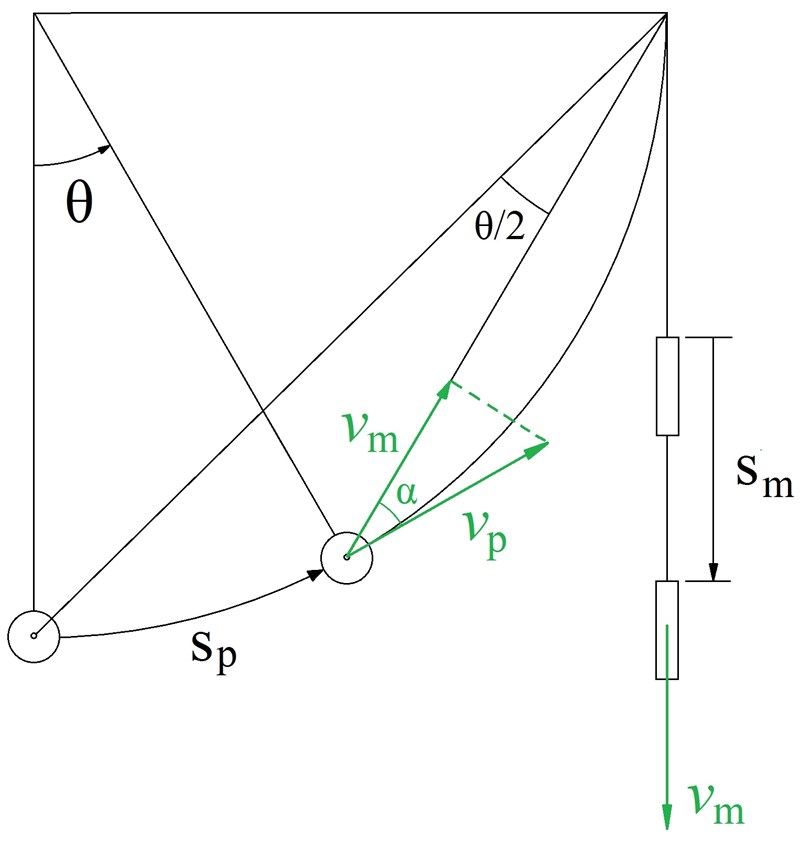
Där randvinkelsatsen gav vinkeln . Vinkeln ges av sinussatsen som:
Vi får att . Detta ger slutligen:
Du kan gå en annan väg och bevisa förhållandet mellan hastigheterna genom att formulera avstånden partikeln och massan färdas som:
Om vi nu deriverar dessa med avseende på tiden får vi:
Vi ser att vilket skulle visas.
Nästa steg är att ställa upp energin för systemet i läge 1 då och läge 2 då och sätta dessa lika med varandra.
Lycka till!
Måste säga det att du visar verkligen klass!
Jag ska göra ett försök:
I läge 1 då är energin:
I läge 2 då är energin:
Vi ska sätta dessa lika med varandra så att,
Har jag tänkt rätt?
Nu har jag kikat lite mer på Sample problemet 3/18 och kommit fram till att
Lösning av systemet ger rad/s, får inte riktigt till det.
Hm, det är några saker du missar här. Först och främst så lagras torsionsfjädern med energi i läge 2. Vid läge noll är vinkeln noll och därför är fjädern ospänd. Sedan har vi att det vertikala avståndet som massan rör sig är:
Om du nu sätter in får du:
Alltså inte det du skrivit. Vidare ser jag att du glömmer potentiella energin hos partikeln då den ökar genom höjden du kallar .
Om vi kombinerar allt får vi:
Läge 1
Läge 2
Gör sedan precis som du gjort tidigare och ansätt samt .
Hoppas detta hjälper.
Helt fantastiskt. Tackar så mycket för hjälpen. Ska nu börja med deluppgift b) och tänker mig att jag ställer upp samma ekvation men låter då . Återkommer om jag fastnar!
EDIT: En till fråga! Vad för verktyg använder du för att rita den oerhört fina figuren?
Jag använder Microsoft paint eller sketch.io när jag ritar bilder.
Den ekvationen består av och och kan inte lösas analytiskt. Du kan hitta en numerisk lösning genom att använda Newton-Rhapson eller dylikt. Jag rekommenderar att du bara plottar i miniräknaren eller geogebra.
Uppgiften ligger trots allt under computer-oriented problems.
Jag löser det nog med hjälp av MATLAB!
Utav ren nyfikenhet, vad talar kvoten om? Försöker se sambandet!
econo skrev:Jag löser det nog med hjälp av MATLAB!
Bra! Matlab är kung.
Utav ren nyfikenhet, vad talar kvoten om? Försöker se sambandet!
Om du tittar på bilden så är kvoten samma ska som cosinus för vinkeln mellan dem. Du kan också förstå det som skalärprodukten av de normerade riktningsvektorerna som löper i hastighetsriktningen.
Din fråga kanske är en annan, jag är osäker. Du kan lista ut att proportionerna mellan vektorernas storlek är beskaffad sådan på flera olika sätt. Jag såg det geometriskt, man kan också härleda genom kinematiskt tvång som jag visade men man kan även trixa lite med vektorer.
Nu fick jag lite problem med ekvationen som består av och .
Följande MATLAB kod:
clear all
syms theta
assume(theta,'positive')
dottheta = 0; kT = 100; m = 5; L = 0.8; M = 8; g = 9.81;
Vm = m*g*L*(1-cos(theta)) %Potential energy, increases with height
Ve = 1/2*kT*(theta)^2 %Potential energy in torsion spring
Tm = 1/2*m*(L*dottheta)^2 %Kinetic energy for mass, m
TM = 1/2*M*(L*dottheta*cos(pi/4-theta/2))^2 %Kinetic energy, M
eqn1 = Vm+Ve+Tm+TM==M*g*L*(sqrt(2)-1)
vinkel = vpa(solve(eqn1,theta)*180/pi,3)
ger . I facit står det . Vet inte redigt hur dem fick det :/
Avståndet som massan rört sig beror på vinkeln. När du definerade eqn1 skrev du att:
VM = M*g*L*(sqrt(2)-1)
Detta stämmer inte, vi har att:
VM = M*g*L*(sqrt(2) - 2*sin(pi/4-theta/2))
Edit: Att du missade detta kanske beror på att jag skrev att den beror på θ^2 och cos(θ) när den också beror på sin(π/4 - θ/2).
Hursomhelst, denna ekvation (eqn1) kommer du inte kunna lösa med 'solve'-funktionen i MATLAB när du skriver den korrekta. Detta eftersom det inte finns någon explicit lösning. Du måste använda en iterativ lösare som exempelvis 'fzero':
func = @(theta) ; M*g*L*(sqrt(2) - 2*sin(pi/4-theta/2)) - kT*theta^2/2 + m*g*L*(cos(theta)-1);
theta = fzero(func,1)
Det jag gjort här är att jag ställt upp en funktion av och jag letar efter vilket värde på vinkeln denna funktion är lika med noll. Det jag gjort är helt enkelt att ta alla termer i din 'eqn1' och flyttat över dem på ett led så att funktionen är lika med noll.
Lite rörigt kanske, fråga om det är något.
Det hade jag missat! Hade tänkt mig att vpasolve funktionen skulle funka men icke. Återigen får jag tacka dig!
Lyckades du ställa upp detta problem med hjälp av vektorer? Jag tyckte att du skulle lösa det med energi för att man inte lär sig lösa det med vektorer förrän i kapitel 6.


