permutation ofch kombinatorik
Hej!
I en figur finns 5 obokstäver från A- E ordnade på en ring med 5 positioner. Hur många sätt kan man ordna 5 bokstäver i en ring med 5 positioner ?
Min lösning : 5! Då jag tänker att det kommer bli som att ordna alla element utav 5 element P(5,5)
Fast i facit ska det vara 5!/5 = 4! ,
skulle någon kunna förklara varför ?
Tack i förväg !
Om du roterar och flyttar alla ett steg åt vänster. Tycker du då att du har en ny unik ring? Om du roterar och flyttar alla ännu ett steg åt vänster. Tycker du då att du har en ny unik ring?
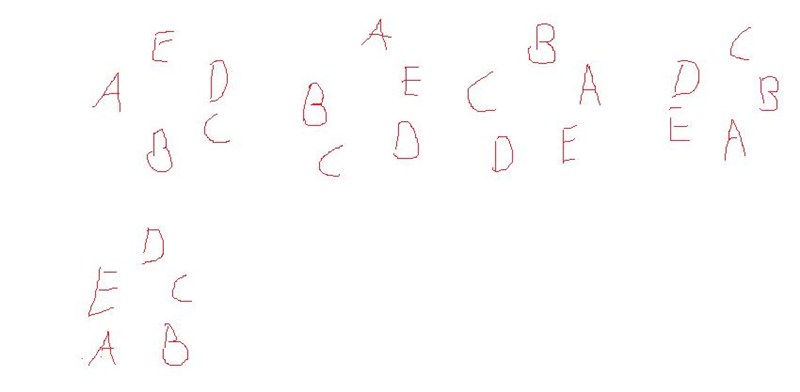
Alla dessa fem ringar är samma ring, bara att vi börjat ringen på olika ställen. Detta gäller för samtliga val av bokstäver. Vi har alltså fått med alla kombinationer fem gånger.
Vi måste därför dividera med 5 för att kompensera för detta
Det hade varit skillnad om de satt på ett led. Då hade det funnits 5! kombinationer.
Ett annat sätt att se det, utan att behöva involvera en (konceptuell) division, är genom att fixera en av bokstävernas position.
Alla ringar kommer ju att innehålla bokstaven A så det betyder ju att alla ringar går att rotera så att A är "längst upp" om man roterar dem så att de ser lite ut som pentagoner. Tänk dig en lista med en massa rader av ringar där A är högst upp i dem alla.
Om A alltid är i toppen så är det egentligen inte en fri position och man har endast val i vilka bokstäver man sätter på de andra positionerna. Det finns 4 positioner för de övriga bokstäverna så 4!
Jag fattade från det här klippet:
https://www.youtube.com/watch?v=gxeP3PeA09I&list=PLmdFyQYShrjfPLdHQxuNWvh2ct666Na3z&index=14




