Poisson-process
Hej!
Låt vara två Poisson-processer med intensiteter . Beräkna , dvs sannolikheten att om .
Vi har ju två fall då det senare är sant, nämligen då eller då .
Jag har då räknat
men svaret är .
Var tänker jag fel?
Tack!
Vilken formel har du använt?
Spontant tycker jag det ser rätt ut. Men när jag använder en kalkylator på nätet får jag din formel att bli 0.4 =2/5, vilket dock fortfarande är fel jämfört med vad du säger att facit uppger
Fibonacci skrev:Vilken formel har du använt?
Ingen jag läst om, utan jag tyckte bara det kändes rimligt såhär. Har försökt skriva en formel som räknar ut sannolikheten för utfall A genom att räkna där utgör hela utfallsrummet.
Hondel skrev:Spontant tycker jag det ser rätt ut. Men när jag använder en kalkylator på nätet får jag din formel att bli 0.4 =2/5, vilket dock fortfarande är fel jämfört med vad du säger att facit uppger
Ojsan, 0.4 är svaret. Då har jag gjort räknefel antar jag. Ska testa igen.
Jag får också 2/5 från din formel. Har för mig att det heter betingad sannolikhet om man ska sätta namn på det.
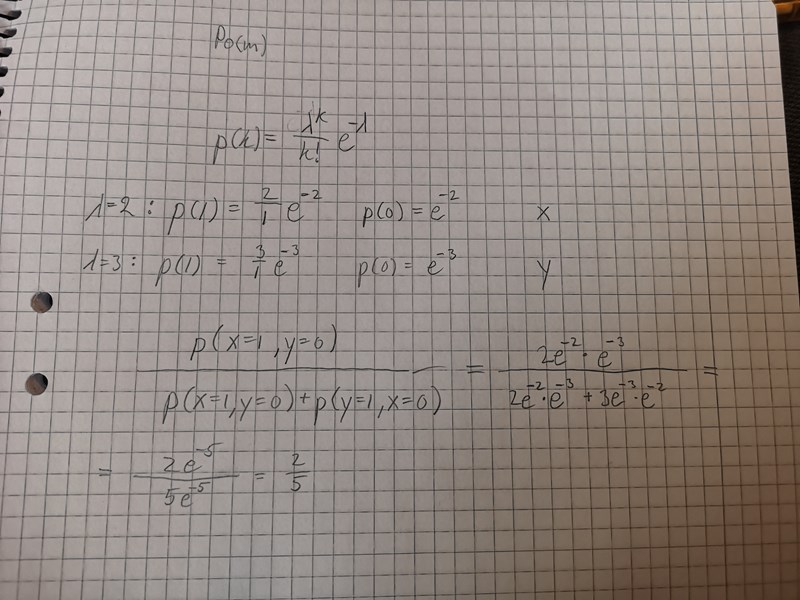
Jag använder Bayes sats och får 2/5=0,4
Fixade det nu, tack!
Hej,
Slumpvariabeln är -fördelad oberoende av slumpvariabeln som är -fördelad. Det ger och samt och så att den sökta sannolikheten enligt Bayes sats blir
Med och blir den sökta sannolikheten
- Om är mycket stort så är det observerade utfallet mycket ovanligt och beräkningen säger att det då är osannolikt att
- Om är mycket liten så är det observerade utfallet väsentligen samma sak som att och beräkningen säger att det är högst troligt att



