Räkna ut omkrets på triangel
Punkten M är mittpunkt på sidan AB i triangeln ABC. Beräkna triangeln ABC:s omkrets, givet att triangeln AMC är liksidig och att |AB| = 12l.e.
svar: 18 + 6*sqrt(3)
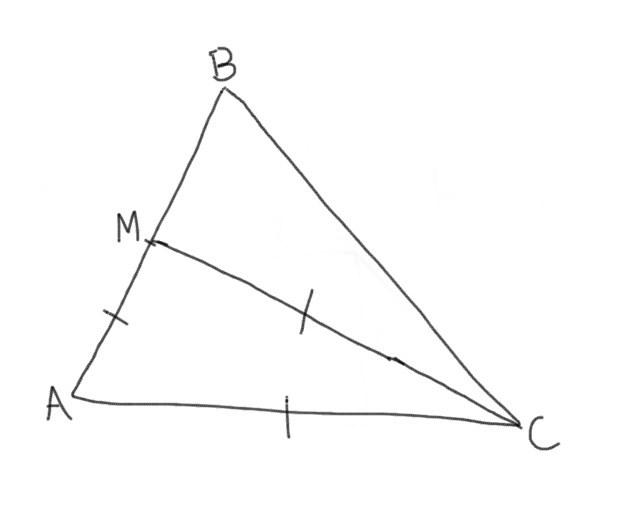
|AB|=12 l.e. Och M är mittpunkt på längden AB, därför måste |AM|=|MB|=6 l.e. Och triangeln AMC är liksidig så |AM|=|MC|=|AC|=6 l.e. Och vinklarna i triangeln AMC måste då vara 60 grader. För att ta reda på längden |BC| så använde jag mig av cosinussatsen. Sedan tog jag och adderade ihop sidorna |AB|+|AC|+|BC|=12+6+|BC|=18+|BC|. Antar att i svaret fick de att längden BC är 6*sqrt(3) men jag får det till något helt annat. Hur löser man den här frågan?
Du har nog tänkt rätt, men använt cosinussatsen felaktigt.
HT-Borås skrev:Du har nog tänkt rätt, men använt cosinussatsen felaktigt.
Får fortfarande fel, såhär använde jag cosinussatsen:
c^2=a^2+b^2-2abcosc
vi applicerar den på frågan:
(|BC|)^2=6*6+12*12-2*6*12*cos(60)
(|BC|)^2=(36+144)-144*cos(60)
(|BC|)^2=180-144*((sqrt(3))/2)
(|BC|)^2=180-72*sqrt(3)
hur har jag använt satsen fel?
nilson99 skrev:
Får fortfarande fel, såhär använde jag cosinussatsen:
c^2=a^2+b^2-2abcosc
vi applicerar den på frågan:
(|BC|)^2=6*6+12*12-2*6*12*cos(60)
(|BC|)^2=(36+144)-144*cos(60)
(|BC|)^2=180-144*((sqrt(3))/2)
(|BC|)^2=180-72*sqrt(3)
hur har jag använt satsen fel?
Ditt värde på cos(60°) är fel.
Om man fortsätter att räkna ut alla vinklarna så visar det sig att vinkeln vid C blir nåt trevligt.




