Två polynomfunktioner f(x) och g(x) är plottade nedan:
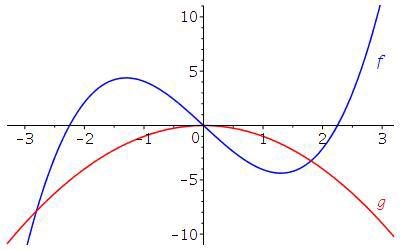
Dessa två polynom kombineras till fyra nya funktioner.
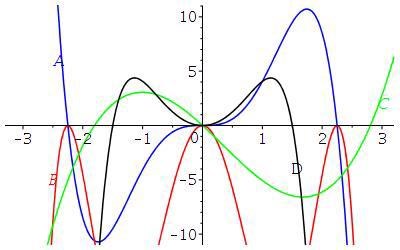
Jag ska ange graferna till följande:

Jag vet inte hur jag ska göra, mitt huve slockna efter att se så många grafer men de andra uppgifterna som liknade denna har jag lyckats med /:
Ta rutat papper och rita upp de fyra funktionerna, en i taget (på vart sitt papper): f(x)+g(x) (kanske enklast), f(x)g(x), etc.
Jag hade räknat fram enstaka punkter och undersökt vilket svarsalternativ som matchar. Är du med på hur sammansättningar som f(g(x)) fungerar?
För att beräkna värden av den sammansatta funktionen väljer vi ett x-värde, t.ex. x=1. Sätt in det i den inre funktionen g(x), dvs läs av g(1) ur grafen. Ser ut att vara -1 ungefär? Alltså g-kurvans y-värde där x=1. Sätt in det värdet i den yttre funktionen, dvs läs av f(-1), vilket ser ut att vara ca 4.
Då vet vi alltså att när x=1, ska sammansättningen ge y=4. Kika bland svarsalternativen, vilken eller vilka uppfyller det? Finns det flera får man räkna fram ytterligare en punkt som kan särskilja alternativen.
(Varning för fula bilder!)
Börja med , samt . För att hitta , markera de områden där och ligger på ungefär samma avstånd från x-axeln, men på olika sidor av den (en ovanför och den andra nedanför). Då bör du få något i stil med:
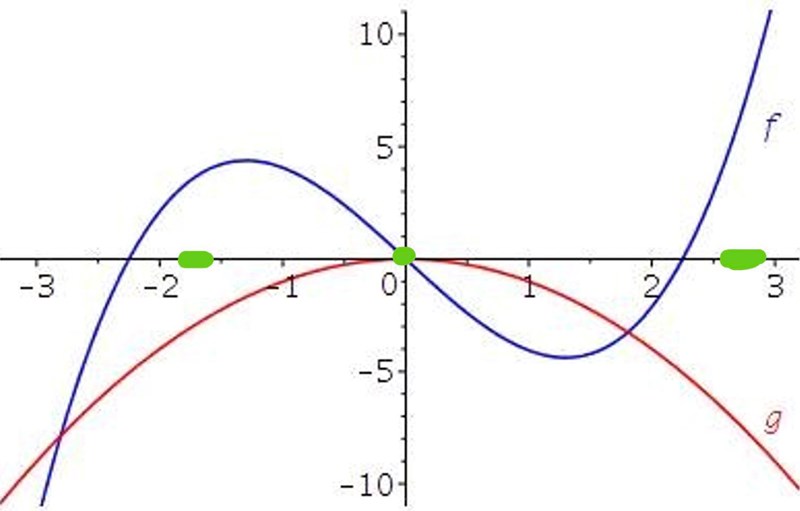
ska alltså ha tre nollställen, ett mellan -2 och -1, ett i origo, och ett mellan 2 och 3. Det finns endast en funktion som uppfyller detta. Om du hade haft fler möjliga alternativ med rätt nollställen, undersök vad som borde hända med summan av funktionsvärdena mellan nollställena. Hamnar den ovanför eller nedanför x-axeln? Sätt en punkt ovanför x-axeln om funktionen bör gå ovanför, och en nedanför om funktionen bör hamna nedanför x-axeln (behöver inte vara fint eller i närheten av den riktiga summan). Då får vi något i stil med:
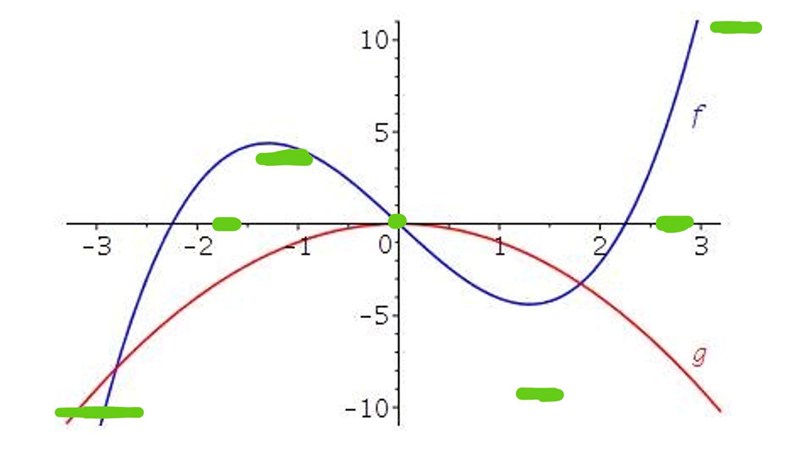
Och vi kan skissa den ungefärliga funktionen:
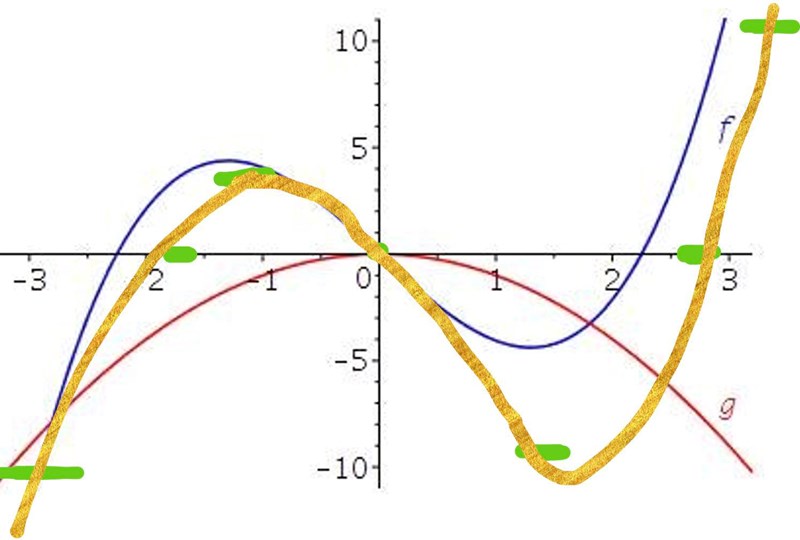
Vars utseende stämmer överens med C.
Sedan är kommer . Här är det bra att tänka på att alla tal gånger noll blir noll. Det innebär att måste ha samma nollställen som dess faktorer, dvs. ett mellan -3 och -2, ett i origo, och ett mellan 2 och 3. Då kvarstår endast alternativ A och B. Vi kan nu göra något liknande som vi gjorde ovan. Vad händer med produkten i de olika intervallen, blir den positiv eller negativ? Vi ritar:
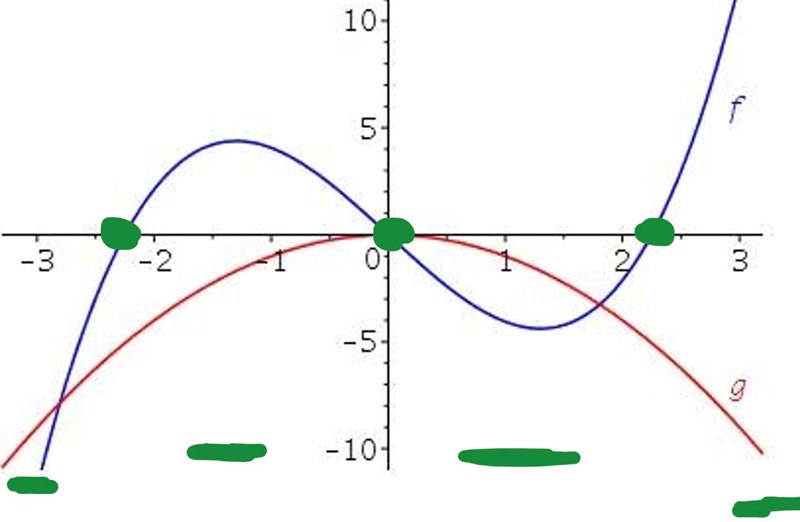
Eftersom g är negativ för alla x (utom origo) får aldrig gå ovanför x-axeln, vilket ger oss alternativ B. Vi kan även skissa fram grafens ungefärliga utseende med hjälp av våra markeringar:
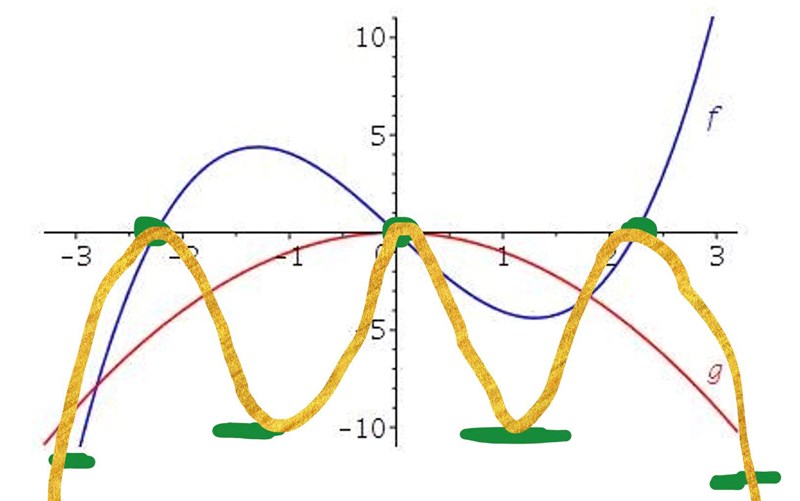
Vilket stämmer med alternativ B.
Då kvarstår och . Vi kan försöka hitta ungefärliga uttryck för f och g, men det lättaste är nog att undersöka nollställena. Välj en punkt på f, säg (enkelt att välja nollställen). Där vet vi att . Vad är då ? Det kan vi läsa av som noll. måste alltså vara ett nollställe till .
Detta räcker för att bestämma vilken funktion som beskriver , men pröva gärna med fler punkter för att få en känsla för sammansatta funktioner. Vad händer då ? ? :)
Det där var otroligt bra svar, tack så jätte mycket !!!





