14 svar

170 visningar

Ygolopot är nöjd med hjälpen

Uppgift angående Riesz

Hej!

Har följande uppgift och behöver lite hjälp med uppgift b:

Har två frågor:

1. Jag vet inte om jag tolkar satsen rätt: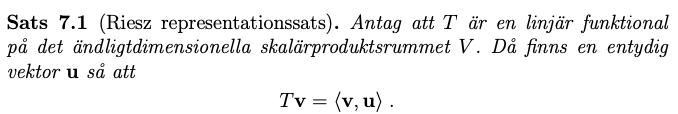

Tolkar Riesz sats som att det för varje v finns en entydig vektor u så att ovan gäller.

2. Jag förstår ärligt talat inte vad jag ska göra riktigt, men ON-basen från uppgiften i a har jag fått till: ${e_{1}, e_{2}} = {1, \sqrt{3} (2 t - 1)}$ vilket jag tror stämmer. Jag tror att jag ska hitta en generell representation så att det i satsen håller. Om a, b, c, och d är skalärer och jag tar en generell vektor: $w = c e_{1} + d e_{2}$ så ska den med en annan generell vektor $u = a e_{1} + b e_{2}$ uppfylla att:

$T w = <w, u> = <c e_{1} + d e_{2}, a e_{1} + b e_{2}> = <c e_{1}, a e_{1} + b e_{2}> + <d e_{2}, a e_{1} + b e_{2}> = c a + d b = T w$

Har att: $T w = T (c e_{1} + d e_{2}) = c T e_{1} + d T e_{2} = c + d \sqrt{3}$

Så $c + d \sqrt{3} = c a + d b, a l l t s å ä r : a = 1 o c h b = \sqrt{3}$

Men detta gör ju w entydig vilket förvisso satsen säger men det gör ju att en entydig vektor w uppfyller $T w = <w, u>$ för alla u i V. Det är på grund av mitt resultat här som jag tvekar på att jag tolkat satsen rätt. Satsen säger ju förvisso inte "för varje v" men säger inte heller att det "för alla v". Kanske är lite otydligt inlägg men famlar lite för har inget facit och jag förstår ju inte riktigt vad det är jag ska göra så jag hoppas jag är lite rätt ute iaf. Hjälp mig gärna att framförallt tolka frågan, det är ju en bra utgångspunkt att förstå den åtminstone ;)

Tack på förhand!

Är ju bra om man läser beviset med... Där står det bland annat:

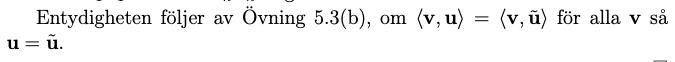
Därmed tolkar jag det som att det är samma unika vektor u som löser $T w = <w, u>$ för alla w i V.

Mot bakgrund av detta tolkar jag uppgiften som att jag ska hitta just den vektor u som löser detta vilket jag tror jag har gjort.

Men som sagt, säg gärna till om jag är fel ute

Det här är aningen för svårt för mig men jag försöker.

Tolkar Riesz sats som att det för varje v finns en entydig vektor u så att ovan gäller.

Ja, men annorlunda uttryckt så betyder det att det alltid finns en vektor som med hjälp av den inre produkten representerar den linjära formen. På samma sätt som det alltid finns en matris för linjära avbildningar mellan ändliga vrum.

Därmed tolkar jag det som att det är samma unika vektor u som löser Tw =<w,u>Tw =w,u för alla w i V.

Ja.

Det är på grund av mitt resultat här som jag tvekar på att jag tolkat satsen rätt. Satsen säger ju förvisso inte "för varje v" men säger inte heller att det "för alla v".

Det är underförstått att att det gäller för alla v i V.

Angående själva tillvägagångssättet så...

Jag vet inte vilken norm de vill att baserna ska vara normerade med... Men de är i alla fall ortogonala.

Vi vill att en likhet ska gälla, nämligen Tv=(v,u). Vad är Tv och vad är (v,u)? (förutom att de är lika med varandra?)

Jag är osäker på om allt ska göras i basen från förra uppgiften...

Visa spoiler

Jo, $T v = v (1) = v_{1} * 1 + v_{0}$

och

$<v, u> = \int_{0}^{1} v u d x = \int_{0}^{1} (v_{1} x + v_{0}) (u_{1} x + u_{0}) d x$ Vilket blir ett uttryck om du integrerar allt med allmänna v och u. Vad ska alltså u1 och u0 vara för att det ska vara lika med v1+v0 på första raden?

Jag har skrivit allt detta i standardbasen {1, x}, och som sagt vet jag inte om vi ska använda din OG bas.

Normen man använder i det här fallet är den vi definierar med den inre produkten, d.v.s. $\|x\|=\sqrt{\langle x,x\rangle}$ , men det tror jag att OP redan klurat ut. (Båda basvektorerna är normerade enligt denna norm).

Det borde inte vara något problem med att använda standardbasen i uppgift b) eftersom uppgiften inte säger något om vilken bas som ska användas. Det som Qetsiyah säger borde alltså stämma.

Om vi inte tar hänsyn till avsikten av frågan så är det väl inte heller smidigare att lösa med ON basen?

Och i sats 7.1, varför skrev de "skalärproduktsrummet" och inte inre produktrummet? Det är väl lite konstigt...

Aha okej, ja det blir ju ett helt annat tillvägagångssätt om jag inte använder ON-basen. Räknade lite på det och fick: Om vi utgår från basen {e_1, e_2} = {1,x} så är en generell vektor: $u = a e_{1} + b e_{2} = a + b t$ , ta en annan generell vektor v = c+dt

Då blir det som du skriver: $T v = c + d$ , och:

$<v, u> = <a + b t, c + d t> = \int_{0}^{1} v u d t = \int_{0}^{1} (a + b t) (c + d t) d t = \int_{0}^{1} (a c + a d t + b c t + b d t^{2}) d t$

= ... = $c (a + \frac{b}{2}) + d (\frac{a}{2} + \frac{b}{3}) = c + d$ , vilket ger a = -2 och b = 6. Så då blir det entydiga u som löser detta: $u = - 2 + 6 t$

Testade detta och det verkar ju uppfylla kraven för Riesz (vilket det såklart bör göra med förutsatt att jag inte räknat fel). Och att det blir ett annat u beror väl alldeles säkert på basen.

Så givet att detta var uppgiften så har jag nog löst det nu. Tack! :)

Qetsiyah skrev:
Om vi inte tar hänsyn till avsikten av frågan så är det väl inte heller smidigare att lösa med ON basen?
Och i sats 7.1, varför skrev de "skalärproduktsrummet" och inte inre produktrummet? Det är väl lite konstigt...

Nej, jag skulle också säga att det bara leder till krångel att använda den beräknade ON-basen.

Jag har faktiskt inte heller hört "skalärproduktsrum" förut, men en Google-sökning visar att flera av landets universitet använder sig av begreppet. Det är väl bara en synonym till inre produktrum.

Qetsiyah skrev:
Om vi inte tar hänsyn till avsikten av frågan så är det väl inte heller smidigare att lösa med ON basen?
Och i sats 7.1, varför skrev de "skalärproduktsrummet" och inte inre produktrummet? Det är väl lite konstigt...

Är väl en smaksak vad som blir lättast men slipper ju hela integral-biten (även om den i detta fall inte var så stökig) om jag tar ON-basen. Samtidigt måste jag ju skapa ON-basen först.

Ygolopot skrev:
Qetsiyah skrev:
Om vi inte tar hänsyn till avsikten av frågan så är det väl inte heller smidigare att lösa med ON basen?
Och i sats 7.1, varför skrev de "skalärproduktsrummet" och inte inre produktrummet? Det är väl lite konstigt...
Är väl en smaksak vad som blir lättast men slipper ju hela integral-biten (även om den i detta fall inte var så stökig) om jag tar ON-basen. Samtidigt måste jag ju skapa ON-basen först.

Å andra sidan måste du ju då ta fram $Te_1$ och $Te_2$ , men som du säger är det väl en smaksak.

Notera också att båda dina svar $e_1+\sqrt{3}e_2$ och $-2+6t$ är rätt och beskriver samma vektor eftersom $e_1+\sqrt{3}e_2=1+\sqrt{3}\cdot\sqrt{3}(2t-1)=-2+6t$ . Båda metoder fungerar alltså.

Hej,

Fråga 1. Din tolkning är fel. Satsen kopplar ihop funktionalen $T$ med en unik vektor $u$ , inte varje vektor $v$ med en vektor $u.$ Att plocka en linjär funktional är alltså samma sak som att plocka en viss vektor och bilda skalärprodukt.

AlvinB: Snyggt! Hade inte testat att översätta dom till samma bas men blir ju tydligt när man gör det så att det är samma sak man räknar på, bara att man är i olika baser. Tack :)

Albiki: Aha!! Grymt, det hade jag faktiskt inte fattat riktigt ännu. Tack!

Jag ser nu i att du egentligen redan visste hur problemet skulle lösas, jag kollade inte din lösning så noga för att den såg konstig ut. Jag visste inte att du använde ON basen. Ursäkta för det hehe

Uppgift b. Den sökta representanten $q_T \in V$ är sådan att

$\displaystyle T(p)=(p,q_{T})=q_{0}^{T}\cdot \int_{0}^{1}p(x)\,dx+q_1^{T}\cdot \int_{0}^{1}xp(x)\,dx.$

Uppgiften är att finna tal $q_0^{T}$ och $q_1^{T}$ så att summan ovan blir lika med talet $p(1)$ .

Eftersom $p(x) = p_0+p_1x$ så blir $p(1) = p_0+p_1$ och explicit beräkning av integralerna ger följande.

$\int_0^{1}p(x)\,dx = p_0+0.5p_1$ samt $\int_0^1 xp(x)\,dx = 0.5p_0+\frac{1}{3}p_1$

vilket resulterar i summan

$\displaystyle q_0^{T}(p_0+0.5p_1)+q_1^{T}(0.5p_0+\frac{1}{3}p_1) = p_0(q_0^{T}+0.5q_1^{T})+p_1(0.5q_0^{T}+\frac{1}{3}q_1^{T}).$

Kravet att detta ska vara lika med $p_0+p_1$ medför det linjära ekvationssystemet

$q_0^{T}+0.5q_1^{T} = 1$ och $q_0^{T}+\frac{2}{3}q_1^{T}=2$

vars lösning är $(q_0^{T},q_1^{T})=(-2,6).$

Den sökta representanten är tydligen polynomet

$q_T(x) = -2+6x$ .

Om du läser igenom beviset av Riesz representationssats så ser du att beviset är konstruktivt, dvs beviset säger hur du kan bestämma vektorn v. Det är ett ganska kort resonemang om jag minns rätt, väl värt att komma ihåg om liknande uppgifter brukar komma på tentan.

Svara Avbryt

Visa senaste svar