Uppgiftsbank-Matematik 3-Integraler
Tanken med denna tråd är att ni ska kunna använda följande uppgifter för att träna och repetera era kunskaper inom momentet "Integraler" i matematik 3 kursen på gymnasiet. Därför har jag skapat en uppgiftsbank med varierande uppgifter från E till A-nivå. Om ni själva skulle vilja dela med er av uppgifter så får ni gärna bygga vidare på uppgiftsbanken inom momentet "Integraler". Kommentarer och inlägg som inte följer instruktionerna bör postas i en separat tråd eller skickas via PM. Detta för att göra tråden mer lättläst och mindre stökig.
Skulle ni hitta några fel eller liknande kan ni kontakta mig via PM här.
Tips: När du läser frågorna, scrolla så att frågan är längst ned på skärmen. Gör först ett eget försök att lösa uppgiften, innan du läser lösningsförslaget.
Min tanke är att strukturen på en post ska se ut som följande:
Nivå: (E, C eller A)
Uppgift: Här skriver du uppgiftens innehåll och fråga/frågor.
Lösning: Här skriver du lösningen till frågan/frågorna.
Skriven av: Inget jag anser måste vara med, men endast om man vill refererar till vem som är uppgiftsskaparen eller var uppgiften kommer ifrån.
Klistrad av Teraeagle, moderator
Nivå: E
Uppgift: Bestäm samtliga primitiva funktioner till
Lösning: , där är en konstant.
För att kontrollera att svaret är korrekt ska gälla, vi kollar: .
Svar:
Skriven av: Jonis10
Nivå: E
Uppgift: Integralen är given
a) Vilken är den övre integrationsgränsen?
b) Vilka är integrationsvariabeln?
Lösning:
a) Den övre integrationsgräsen motsvarar talet som är markerat i blått: , vilket motsvarar 7. Svar: 7
b) Integrationsvariabeln är markerat i rött: se a) vilket motsvarar . Svar:
Skriven av: Jonis10
Nivå: E
Uppgift: Anta att en befolkning miljoner ökar med hastigheten , där är antal år efter 2018.
a) Bestäm om befolkningen var 15 miljoner år 2018.
b) Med hur många invånare ökar befolkningen mellan 2018 och 2020.
Lösning:
a) , där
Svar:
b) Befolkningsökningen mellan 2018 och 2020 kan beräknas följande:
Svar: Ca 0,87 miljoner
Skriven av: Jonis10
Nivå: E
Uppgift: Beräkna integralen
Lösning:
Svar: 80
Skriven av: Jonis10
Nivå E:
Uppgift: Ange alla primitiva funktioner till
Lösning: , där är en konstant.
För att kontrollera att de är korrekt ska gälla. Vi kollar: .
Svar:
Skriven av: Jonis10
Nivå: C
Uppgift: Funktionen . Bestäm den primitiva funktionen som uppfyller villkoret och beräkna .
Lösning: , där .
Det ger att .
Svar:
Skriven av: Jonis10
Nivå: C
Uppgift: Bestäm konstanten så att
Lösning:
Svar:
Skriven av: Jonis10
Nivå: C
Uppgift: För en funktion har egenskaperna att och . Bestäm .
Lösning:
, där är en konstant. Detta medför att:
Svar:
Skriven av: Jonis10
Nivå: C
Uppgift:
Figuren visar grafen till en funktion det vill säga en primitiva funktionen till . Bestäm 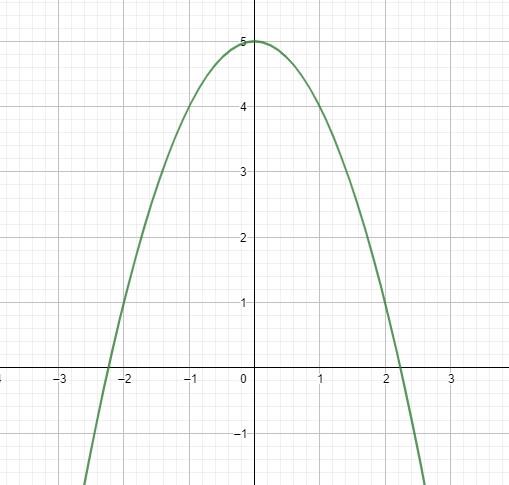
Lösning: , Svar: 3
Skriven av: Jonis10
Nivå: C
Uppgift: Bestäm en primitiv funktion till
Lösning: , låt t.ex.
Svar: T.ex.
Skriven av: Jonis10
Nivå: A
Uppgift: För en funktion där . I en punkt Q som ligger på kurvan är en tangent dragen. Tangenten bildar tillsammans med de positiva koordinataxlarna och punkten Q en parallelltapets. Bestäm punktens Q:s x-koordinat så att arean blir 0,5 a.e.
Lösning: Anta att punkten Q har koordinaterna där .
vilket motsvarar lutningen för tangenten. Tangentens ekvation blir då: .
Där efter går det att ställa upp ekvationen:
Svar: Punktens Q:s x-koordinat är
Skriven av: Jonis10
Nivå: A
Uppgift: Jonathan kör med hastigheten 90 km/h när han plötsligt ser sin fysik lärare 90 meter bort som är på väg över gatan. Hur mycket ska hastigheten minska per sekund så att han inte precis så kör sin lärare.
Lösning: Anta att retardation är det ger att . Hastigheten när han stannar är måste vara noll vilket ger efter tiden: .
Detta ger ekvationen:
Svar: Hastigheten ska minska med
Skriven av: Jonis10
Nivå: A
Uppgift: Kurvan innesluter tillsammans med x-axeln ett område. Hur stor andel av områdets area kan triangeln högst uppta?
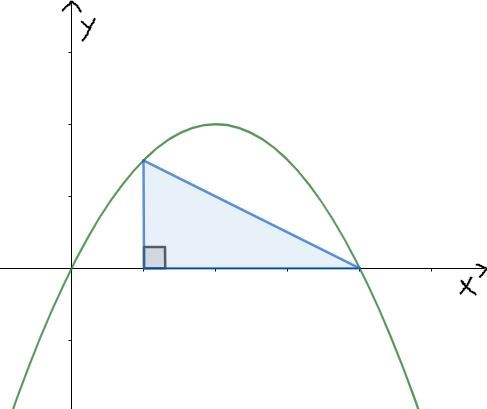
Lösning: För att börja med att vi ta fram nollställena för kurvan . .
Arean som kurvan innesluter är detsamma som: a.e.
I bilden ovan syns en rätvinklig triangeln om triangelns vänstra hörn på x-axeln har koordinaten där . Basen på den rätvinkliga triangeln är då det samma som och höjden .
Detta ger att:
Nu söker vi den maximala arean:
(minimipunkt)
(maximipunkt)
a.e.
Förhållandet:
Svar:
Skriven av: Jonis10
Nivå: A
Uppgift: Bestäm så att uttrycket där blir så litet som möjligt.
Lösning:
,
(minimipunkt)
Svar:
Skriven av: Jonis10
Nivå: A
Uppgift: Bilden visar grafen för där . Längden för hjälplinjerna är 1 l.e. Bestäm förhållande mellan areorna och .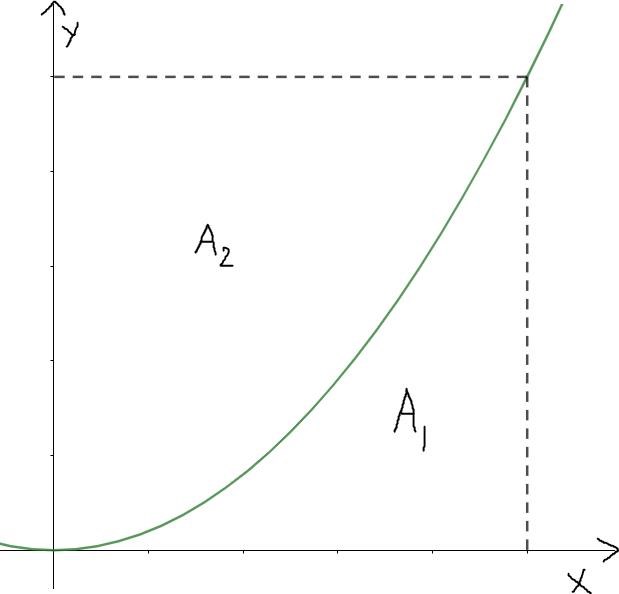
Lösning: Om bredden på rektangeln är 1 l.e. medför det att höjden är dvs en kvadrat.
Detta ger att a.e.
Arean av rektangeln ges av , det med för att
Det ger förhållandet:
Svar:
Skriven av: Jonis10 , notering: för den som vill undersöka lite mer kan sätta bredden till t.ex. l.e. och undersöka vad som händer med förhållande då.


