Variabelsubstitution, hitta Integral genom att förlänga bråk
Hej
Jag 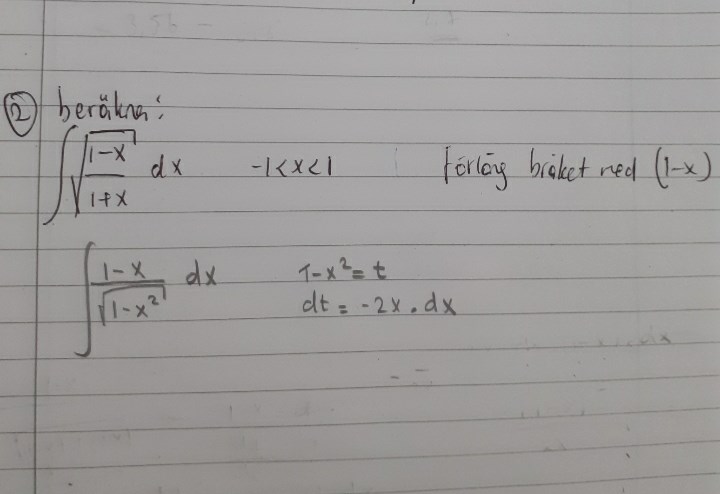 har försökt att lösa det, men lyckades inte. Kan någon hjälpa mig? Tack på förhand
har försökt att lösa det, men lyckades inte. Kan någon hjälpa mig? Tack på förhand
Om du utgår från ditt utvecklade uttryck nederst i din uträkning, så kan du sätta x=sinu
Vad får du om du utvecklar uttrycket nu och gör integralen med avseende på u, dvs du
Vilka integrationsgränser får du nu i uttryckt i vinkeln u (i radianer) ?
Henning skrev:Om du utgår från ditt utvecklade uttryck nederst i din uträkning, så kan du sätta x=sinu
Vad får du om du utvecklar uttrycket nu och gör integralen med avseende på u, dvs du
Vilka integrationsgränser får du nu i uttryckt i vinkeln u (i radianer) ?
Tackar
Jag har inte förstått varför man ska sätta ×=sinu
Du märker det då du jobbar med beräkningarna - det blir hyfsat enkelt.
Och du får en intressant faktor då du deriverar med avseende på u -
Henning skrev:Du märker det då du jobbar med beräkningarna - det blir hyfsat enkelt.
Och du får en intressant faktor då du deriverar med avseende på u -
Tack så mycket. Har löst det genom arcsinx ( vet inte om du menade denna väg, men när du sa sinx har jag sett derivatan av arcsinx efter förlängning med bråket. Sedan löste jag uppgiften (den andre termen) med hjälp av variabelsubstition . Svaret blev rätt enligt facit.
Tack så mycket
Henning skrev:Du märker det då du jobbar med beräkningarna - det blir hyfsat enkelt.
Och du får en intressant faktor då du deriverar med avseende på u -
Jag visar min lösningsvariant - kan vara av intresse även för andra läsare
Integrationsgränserna för de båda variablerna blir:
Uttrycket i x under integraltecknet är:
Med x=sin u blir det nu: , som kan förenklas till
Nu ser integralen ut så här:
Efter framtagning av primitiv funktion får vi:
Lite trixigt - men det speciella knepet var att gå över till en trigonometrisk funktion vid variabelsubstitutionen
Henning skrev:Henning skrev:Du märker det då du jobbar med beräkningarna - det blir hyfsat enkelt.
Och du får en intressant faktor då du deriverar med avseende på u -
Jag visar min lösningsvariant - kan vara av intresse även för andra läsare
Integrationsgränserna för de båda variablerna blir:
Uttrycket i x under integraltecknet är:
Med x=sin u blir det nu: , som kan förenklas till
Nu ser integralen ut så här:
Efter framtagning av primitiv funktion får vi:
Lite trixigt - men det speciella knepet var att gå över till en trigonometrisk funktion vid variabelsubstitutionen
Tack så mycket.

