Vilken är den andra roten?
Hej!
Jag undrar hur man löser denna uppgift, själv har inte så mycket att säga om den infon som jag får därför skulle det underlätta om någon kunde hjälpa mig!
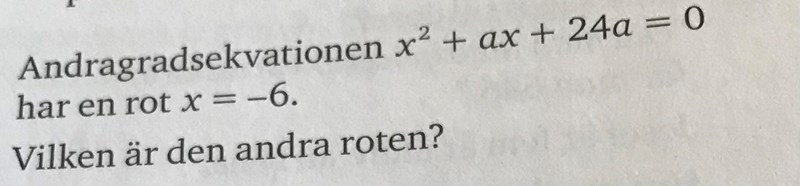
Om du kallar den sökta roten för x=b, så kan du skriva ekvationen på
denna form:
När du sedan utvecklar vänstra ledet så kan du jämföra det med vänstra ledet i
Detta ger dig två ekvationer i a och b ur vilket ekvationssystem du kan få fram bl a b, dvs den andra roten
Stämmer det hittills?
Nej, du har gjort någon felräkning då du multiplicerar parenteserna
Vilken ordning tar du vid multiplikation?
Den första termen i första parentesen gånger den första termen i den andra
Och sedan den första termen i den första parentesen gånger den andra termen i parentes två ?
Du bör ha något system
Ser det bättre ut?
Nu är det rätt.
Du kan nu placera om termerna så att x-termerna står ihop
dvs
För att jämföra med den givna ekvationen
Kan du se hur du kan komma vidare ? Observera att du har två obekanta, a och b
Man kan använda pq formeln men min fråga är om man kan använda den trots att det står två variabler med 6+bx och -6 eller om man ska använda en helt annan formel?
pq-formeln ger nog ingen framgång här
Men vi har ju två andragradsekvationer som ska vara lika, och då kan vi jämföra koefficienterna (talen) framför x-termerna med varandra samt de konstanta talen med varandra
Då får vi två ekvationer med två obekanta vilket är lösbart.
Dvs 6+b = a ...(1)
Vad blir den andra ekvationen ?
x - 6b?
Nej - den konstanta termen i den första ekvationen är -6b och i den andra 24a
Dvs du får sambandet -6b=24a ..(2)
Nu har du ett ekvationssystem med två variabler.
Hur löser du det ?
Henning skrev:pq-formeln ger nog ingen framgång här
Men vi har ju två andragradsekvationer som ska vara lika, och då kan vi jämföra koefficienterna (talen) framför x-termerna med varandra samt de konstanta talen med varandra
Då får vi två ekvationer med två obekanta vilket är lösbart.
Dvs 6+b = a ...(1)
Vad blir den andra ekvationen ?
Vart får du 6+b = a, ifrån? Förstår den andra ekvationen då det bara är konstanterna men denna var lite klurigare...
Henning skrev:Nu är det rätt.
Du kan nu placera om termerna så att x-termerna står ihop
dvsFör att jämföra med den givna ekvationen
Kan du se hur du kan komma vidare ? Observera att du har två obekanta, a och b
Vi har de två ekvationerna ovan och jämför koefficienterna framför x-termerna
I den övre är det: (6+b)
Och i ursprungsekvationen är det a
Okej?
Yes, nu hänger jag med!
6+b=a
-6b=24a
Ska man få a och b ensamt och lösa det som ett vanligt ekvationssystem?
Ja, du kan lösa det som ett vanligt ekvationssystem
Gör gärna det - så kan alla som följer detta se hur man kan göra
Om jag använder additionsmetoden får jag, 6+-6 vilket är 0, blir då b 0 också eller?
Nej det är fel
Kan du visa hur du gör
6+b=a
-6b=24a
02b=25a
Är medveten om att detta inte rätt, använde additionsmetoden men det har blivit något knas däremellan...
Jag tycker att den sk substitutionsmetoden blir enklare
Dvs med ekv (2) -6b=24a fås b=-4a vilket du kan sätta in i ekv (1)
Ekv(1) 6+b=a ger då : 6+(-4a)=a, vilket ger
Och slutligen:
Vilket är rot nr två
Undrar varför man inte multiplicerar -1 på den första ekvationen är det för att den redan är negativ eller att den automatiskt har blivit substituerad?
Hur menar du i detalj ?
Alltså har lärt mig att man har två ekvationer i ett ekvationssystem och för att få ut en av variablerna så brukar man multiplicera en av ekvationerna med -1 för att därmed enklare få ut den andra ekvationen.
Jag tror att din metod inte fungerar så bra i alla lägen.
Substitutionsmetoden fungerar alltid och i detta fall ger den en snabb lösning
Se teori här
Nu har ni väl krånglat till det rejält!
Lös ut a genom att sätta in x=-6:
(-6)2+a(-6)+24a=0
36-6a+24a=0
18a=-36
a=-2
Sätt sedan in a i den ursprungliga formeln och lös ut x (varav det ena svaret blir x=-6 så som framgår av frågan)!


