10 cupcakes på 4 sätt
Hej, jag vet inte alls vad jag ska göra på 1162. Facit ritade upp streck och prickar med färg och allt möjligt. Så min uträkning är helt fel. 
Tips:
Rita tio stjärnor i en lång rad. Varje stjärna symboliserar en cupcake.
Nu kan du rita tre "avdelare" i form av vertikala streck.
Dessa avdelare symboliserar gränserna mellan olika dekorationer.
Frågan är nu på hur många sätt du kan placera dessa avdelare om alla cupcakes ska ha en dekoration.
Orsaken till att jag kallar det stjärnar och streck är att metoden ofta kallas "stars and bars".
Så någonting så här. Så jag har 10 stjärnor för 10 cupcakes. Sedan 3 streck för det bildar 4 grupper som står för alla sorters dekorationer. Detta leder till att man tar 13 över 3, då 10 cupcakes + 3 streck är lika med 13. Är det rätt?
Kan du förklara när man använder den här metoden ”starts and bars”?

Det är rätt, givet att man inte kräver att alla dekorationer skall vara representerade.
Jag förstår inte riktigt det här sättet att räkna. Så nu kan det vara så att uppdelningen mellan dekorationerna är 4,2,4,0?
Hejsan266 skrev:Jag förstår inte riktigt det här sättet att räkna. Så nu kan det vara så att uppdelningen mellan dekorationerna är 4,2,4,0?
Ja, även 0,0,0,10 - placera alla | på position 1-3.
Här är ett utdrag från min kommande "kioskvältare"...

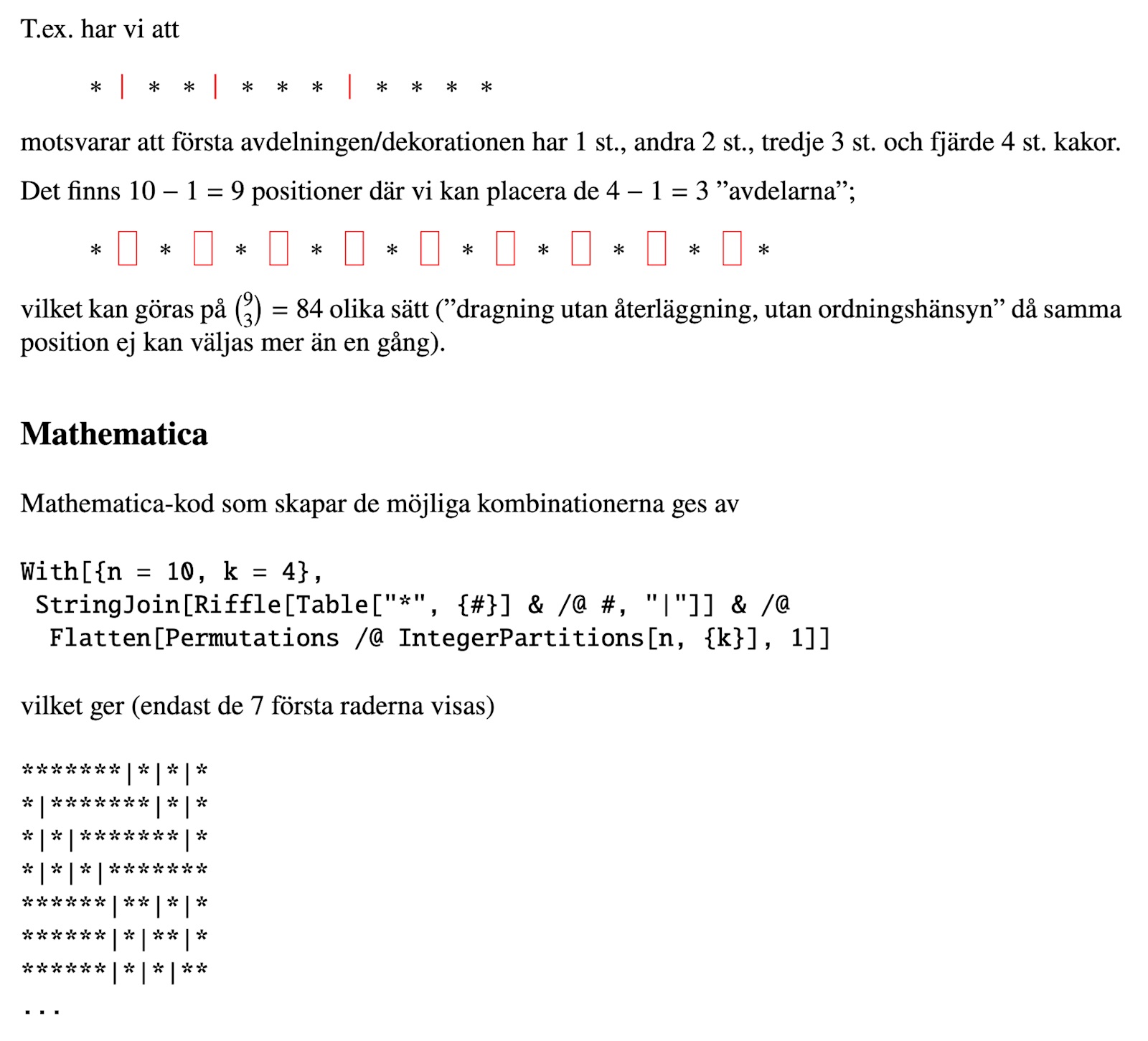


Jag förstår inte riktigt delen där det står 10-1=9 och 4-1=3. Är det inte bara 10 cupcakes och 3 avdelare?
Som jag läser det, så har Trinity2 helt enkelt fel.
Om man bara får placera avdelare i de röda rutorna så måste varje grupp, varje sorts dekoration, ha minst en cupcake.
Det kravet har ingen ställt.
EDIT: Fel av mig, som Gustor påpekade.
Trinity2 behandlar grupper med storlek noll under rubrik Mathematica. (Jag föreslår ändå en annan formulering vid de röda rutorna.)
Man kan också tänka att man har tio stjärnor och tre streck (avdelare) som ska ordnas. Det finns (10+3)! sätt att ordna 13 objekt, och eftersom 10 av dem är av samma typ och de andra tre är av en annan typ behöver vi dela med 10! och med 3! för att inte räkna samma sekvenser flera gånger. Vi får
.
Ett annat sätt, om vi tänker på HL ovan, är att vi placerar tio stjärnor på 13 lediga positioner. Vi kan göra det på sätt. Avdelarnas/streckens tre positioner är då entydigt bestämda.
Tillägg: 13 feb 2025 21:36
Trinity2 behandlar fallet då vi tillåter 0 dekorationer i slutet av inlägget.
Bra synpunkter fråm Bubo och Gustor. Bif. omdisponerad text;
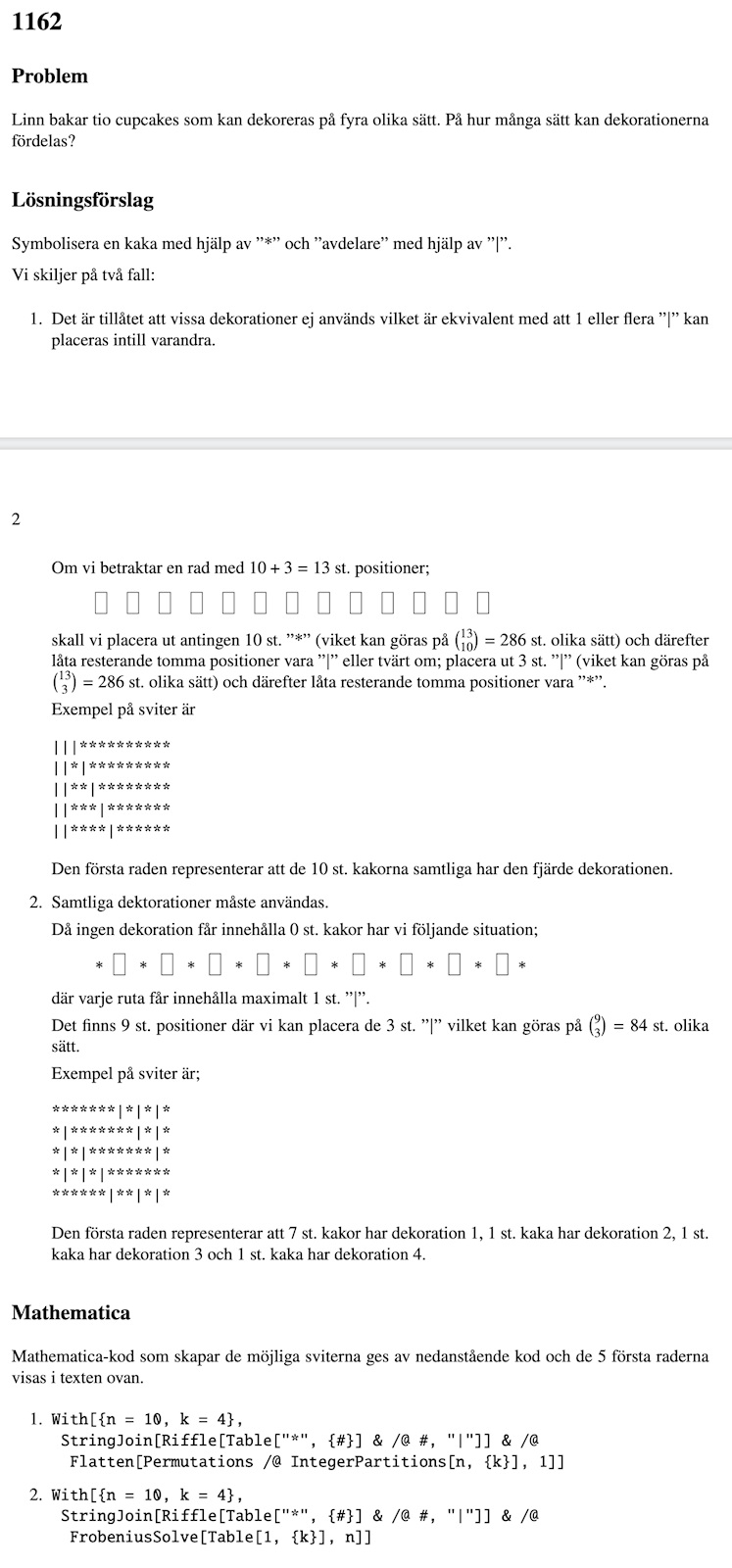
Jag försöker räkna om uppgiften, så i denna uppgift behöver jag inte använda alla 4 sätten att dekorera eftersom det står "kan". Då räknar jag med fall 2, antar jag.
Om jag skulle behöva förklara detta för någon annan. Hur skulle jag förklara att jag har 3 streck istället för 4 när det finns fyra grupper. Men väljer att räkna med 10 cupcakes istället för 10-9.
Jag tycker att följande är ett bra sätt att tänka:
Du har 13 positioner på vilka du ska placera ut 10 cupcakes och 3 avdelare.
En möjlig sådan är
|||********** (Alla har dekoration 1)
En annan är
**********||| (Alla har dekoration 4)
Antalet sätt att göra detta är lika många som att välja ut 3 positioner av 13 möjliga för avdelarna.
Detta är när alla cupcakes ska ha en dekoration.
=======
Om det vore OK att ha cupcakes utan dekoration så skulle det bli 10 stjärnor och 4 avdelare, t ex.
||||********** (Alla saknar dekoration)
**********|||| (Alla har dekoration 4)
13 för att du placerar 10 stjärnor och 3 avdelare, vilket tillsammans är 13 objekt. De kan stå i vilken ordning som helst.
Om du istället tänker att du börjar med tio stjärnor och ska placera ut 3 avdelare, så är det riktigt att den första kan placeras på 11 olika ställen (början, slutet eller i något av de 9 mellanrummen).
Därefter har du en rad av 11 objekt och kan placera nästa avdelare först, sist, eller mellan vilket som helst av de nu 10 mellanrummen. Totalt 12 sätt.
Den sista avdelaren kan placeras på 13 sätt.
Ordningen av dessa spelar ingen roll, så vi behöver dela med 3! för att inte räkna samma kombination flera gånger.
Då får vi sätt. Samma som vi fick med den andra metoden.
Så om jag skulle göra en presentation av denna uppgift och förklara det för andra som aldrig stött på denna metod, skulle detta vara en bra förklaring? Finns det någonting jag borde utveckla eller är fel?
""Stars and bars" är en bra metod för att räkna ut på hur många sätt man kan dela in saker i olika grupper. I denna uppgift kommer stars att vara cupcakesen och barsen vara det som delar upp dekorationerna. 3 eftersom det ger 4 grupper och 10 stars för att det finns 10 cupcakes. Tillsammans har vi 13 objekt som kan stå i vilken ordning som helst. När vi använder 13 objekt finns möjligheten att vissa dekorationer inte används, eftersom vissa bars inte är positionerade mellan två stjärnor och i andra fall finns två bars mellan samma två stjärnor. För att lösa uppgiften använder vi 13 över 3 eller 13 över 10 för att ta reda på hur många sätt jag kan placera 3 bars alternativt placera 10 stjärnor.
Om alla dekorationer måste användas tar man 9+3=12 eftersom barsen måste placeras mellan två stjärnor. Uträkningen blir då 12 över 3 eller 12 över 9. Sedan om uppgiften skulle gjort det möjligt för vissa cupcakes att inte dekoreras skulle det bli 10+4. Uträkning 14 över 10 eller 14 över 4. Men detta gäller inte för denna uppgift."
Bra att du poängterar att det kan vara noll bakelser/stjärnor mellan avdelarna. Jag skulle ge pluspoäng om du förklarar tydligt hur ett arrangemang av de 13 objekten motsvarar en unik kombination av dekorationer, gärna genom ett exempel (alltså typ "det som står till vänster om första avdelaren är de bakelser som får dekoration ett, de som står mellan första och andra avdelaren får dekoration två, osv.) samt att du förklarar hur man kan tänka på det på olika sätt (arrangera alla 13 objekten direkt alternativt placera in avdelare mellan 10 objekt som jag beskrev tidigare).
Så jag ska berätta om ett exempel på hur cupcaksen kan arrangeras?
Jag behöver också lämna in en lösning som mitt betyg hänger på. Ser detta bra ut eller finns det något som kan förbättras?

Hejsan266 skrev:Så jag ska berätta om ett exempel på hur cupcaksen kan arrangeras?
Jag behöver också lämna in en lösning som mitt betyg hänger på. Ser detta bra ut eller finns det något som kan förbättras?

Hejsan266 skrev:Om alla dekorationer måste användas tar man 9+3=12 eftersom barsen måste placeras mellan två stjärnor. Uträkningen blir då 12 över 3 eller 12 över 9. Sedan om uppgiften skulle gjort det möjligt för vissa cupcakes att inte dekoreras skulle det bli 10+4. Uträkning 14 över 10 eller 14 över 4. Men detta gäller inte för denna uppgift."
TACK! Jag ska ändra på det.
Är detta (stycket) verkligen korrekt? Jag försöker förklara detta i inlämningen men får inte det att gå ihop. Trinity2 har skrivit i #10 att det ska vara 9 över 2 och inte 12 över 3, om jag har förstått det rätt. Det beror väl på att 12 över 3 möjliggör för vissa dekorationer att inte användas?
14 över 10 är väl ändå korrekt?
Hejsan266 skrev:Hejsan266 skrev:Om alla dekorationer måste användas tar man 9+3=12 eftersom barsen måste placeras mellan två stjärnor. Uträkningen blir då 12 över 3 eller 12 över 9. Sedan om uppgiften skulle gjort det möjligt för vissa cupcakes att inte dekoreras skulle det bli 10+4. Uträkning 14 över 10 eller 14 över 4. Men detta gäller inte för denna uppgift."
TACK! Jag ska ändra på det.
Är detta (stycket) verkligen korrekt? Jag försöker förklara detta i inlämningen men får inte det att gå ihop. Trinity2 har skrivit i #10 att det ska vara 9 över 2 och inte 12 över 3, om jag har förstått det rätt. Det beror väl på att 12 över 3 möjliggör för vissa dekorationer att inte användas?14 över 10 är väl ändå korrekt?
Jag kommer ej ihåg exakt vad jag skrev men det beror säkert på om man tillåter att något fack skall vara tomt eller ej.
Ja, kollade på en video och det var det de sa så.
En sista fråga. Om jag lägger till en grupp med inga dekorationer blir det 4 bars. Lösningen blir då 14!/(10!4!), ellerhur?
Hejsan266 skrev:Ja, kollade på en video och det var det de sa så.
En sista fråga. Om jag lägger till en grupp med inga dekorationer blir det 4 bars. Lösningen blir då 14!/(10!4!), ellerhur?
Din lösning innehåller redan fallet då vissa dekorationer ej är använda på kakorna, eller menar du att exakt 1 av de 4 dekorationerna inte skall vara använd? Jag förstår ej helt.



