2024 fråga 18
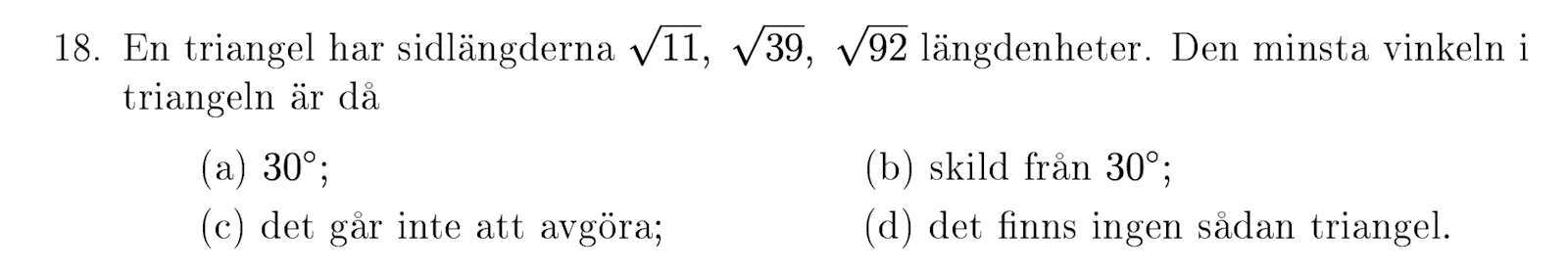
Triangelolikheten säger att 2 sidor måste vara strikt större än den tredje.
, hur ska man kontrollera att detta är sant? Är det tydligt redan som det är ?
Hur ska man annars angripa detta problem ?
Jag antar att miniräknare inte är tillåten.
Om vi kvadrerar får vi i vänsterledet
.
För att detta ska vara större än HL, som är , måste
.
Men .
Alltså är , och rätt svar är (d).
Och man börjar med uteslutningsmetoden. Det är lått att fördubbla ens chans att välja rätt svar:
Alternativet 30 grader stämmer inte.
Alternativ (c) stämmer inte heller.
Sedan kolla (d). Längsta sidan √92 = 2√23 som är uppenbart lite mindre än 10, ungefär 9,6. Det är inte lika lätt att uppskatta en tillräckligt låg gräns för summan av de två korta sidorna , så man får nog göra som Gustor ovan.
Så här i lugn och ro, samt med papper och penna går det att lösa med cosinussatsen.
Om jag vill räkna ut vinkeln som står mot sidan får jag:
För att triangeln skall existera måste alltså 39*92 > 3600.
Det kan man konstatera utan miniräknare.
(Sedan skall man ju ha sinnesnärvaro att prova den här lösningen och lite "tur" att siffrorna är så snälla. Det senare känns inte som en slump.)
Gustor skrev:Jag antar att miniräknare inte är tillåten.
Om vi kvadrerar får vi i vänsterledet
.
För att detta ska vara större än HL, som är , måste
.
Men .
Alltså är , och rätt svar är (d).
Bra sätt att jämföra storheterna.
Varför vet vi att rätt svar är d) bara för att VL > HL ?
2 av triangelns sidor är längre än den tredje? Det är väl inte tillräckligt för att säga d)?
Pieter Kuiper skrev:Och man börjar med uteslutningsmetoden. Det är lått att fördubbla ens chans att välja rätt svar:
Alternativet 30 grader stämmer inte.
Alternativ (c) stämmer inte heller.
Håller med om den metoden.
Hur vet du att dem 2 ej stämmer, förklara hur du resonerar tack.
Korra skrev:Pieter Kuiper skrev:Och man börjar med uteslutningsmetoden. Det är lått att fördubbla ens chans att välja rätt svar:
Alternativet 30 grader stämmer inte.
Alternativ (c) stämmer inte heller.Håller med om den metoden.
Hur vet du att dem 2 ej stämmer, förklara hur du resonerar tack.
Summan av de 2 kortare sidorna kan aldrig vara mindre än den längsta sidan.
Korra skrev:Pieter Kuiper skrev:Och man börjar med uteslutningsmetoden. Det är lått att fördubbla ens chans att välja rätt svar:
Alternativet 30 grader stämmer inte.
Alternativ (c) stämmer inte heller.Håller med om den metoden.
Hur vet du att dem 2 ej stämmer, förklara hur du resonerar tack.
Det är klart att det går att avgöra vad den minsta vinkeln är om sidornas längder är givna, så (c) kan strykas.
Och om tittar på den här med sidor på typ 9,6 längdenheter och drygt 6 och typ 3,5 då är den mycket långsmal (om den existerar överhuvudtaget), den minsta vinkeln skulle vara klart mindre än 30o.
Korra skrev:Gustor skrev:Jag antar att miniräknare inte är tillåten.
Om vi kvadrerar får vi i vänsterledet
.
För att detta ska vara större än HL, som är , måste
.
Men .
Alltså är , och rätt svar är (d).
Bra sätt att jämföra storheterna.
Varför vet vi att rätt svar är d) bara för att VL > HL ?
2 av triangelns sidor är längre än den tredje? Det är väl inte tillräckligt för att säga d)?
Jag vet inte vad i hela friden jag gjorde där i slutet, men , så VL > HL, dvs.
.
Ursäkta förvirringen.
Tillägg: 7 apr 2025 23:47
Det går tydligen inte så bra för mig i den här tråden.

https://www.google.com/search?q=sqrt(11)+sqrt(39)-sqrt(92)
Det är lite elakt med uppgiften att det är så nära. Men cosinusregeln var relativt lätträknat (sictransit i #4).
PATENTERAMERA skrev:
Från det kan vi dra slutsatsen att vi inte kan bilda någon triangel. Just för att kortsidorna är kortare än långsidan.
Korra skrev:PATENTERAMERA skrev:Från det kan vi dra slutsatsen att vi inte kan bilda någon triangel. Just för att kortsidorna är kortare än långsidan.
Så är det! Fördelen med att ge sig på problemet med cosinussatsen är att om det gått att bilda en triangel hade du fått vinkeln. Alternativt, som i det här fallet, kunde man konstatera att cosinus inte kan bli större än 1.
sictransit skrev:Så här i lugn och ro, samt med papper och penna går det att lösa med cosinussatsen.
Om jag vill räkna ut vinkeln som står mot sidan får jag:
För att triangeln skall existera måste alltså 39*92 > 3600.
Det kan man konstatera utan miniräknare.
(Sedan skall man ju ha sinnesnärvaro att prova den här lösningen och lite "tur" att siffrorna är så snälla. Det senare känns inte som en slump.)
Jag gillar denna metod. Hur räknar du ut det utan miniräknare?
Korra skrev:sictransit skrev:Så här i lugn och ro, samt med papper och penna går det att lösa med cosinussatsen.
Om jag vill räkna ut vinkeln som står mot sidan får jag:
För att triangeln skall existera måste alltså 39*92 > 3600.
Det kan man konstatera utan miniräknare.
(Sedan skall man ju ha sinnesnärvaro att prova den här lösningen och lite "tur" att siffrorna är så snälla. Det senare känns inte som en slump.)
Jag gillar denna metod. Hur räknar du ut det utan miniräknare?
Eller uppställning.
Pieter Kuiper skrev:Korra skrev:sictransit skrev:Så här i lugn och ro, samt med papper och penna går det att lösa med cosinussatsen.
Om jag vill räkna ut vinkeln som står mot sidan får jag:
För att triangeln skall existera måste alltså 39*92 > 3600.
Det kan man konstatera utan miniräknare.
(Sedan skall man ju ha sinnesnärvaro att prova den här lösningen och lite "tur" att siffrorna är så snälla. Det senare känns inte som en slump.)
Jag gillar denna metod. Hur räknar du ut det utan miniräknare?
ahhhh clever
Tackar





