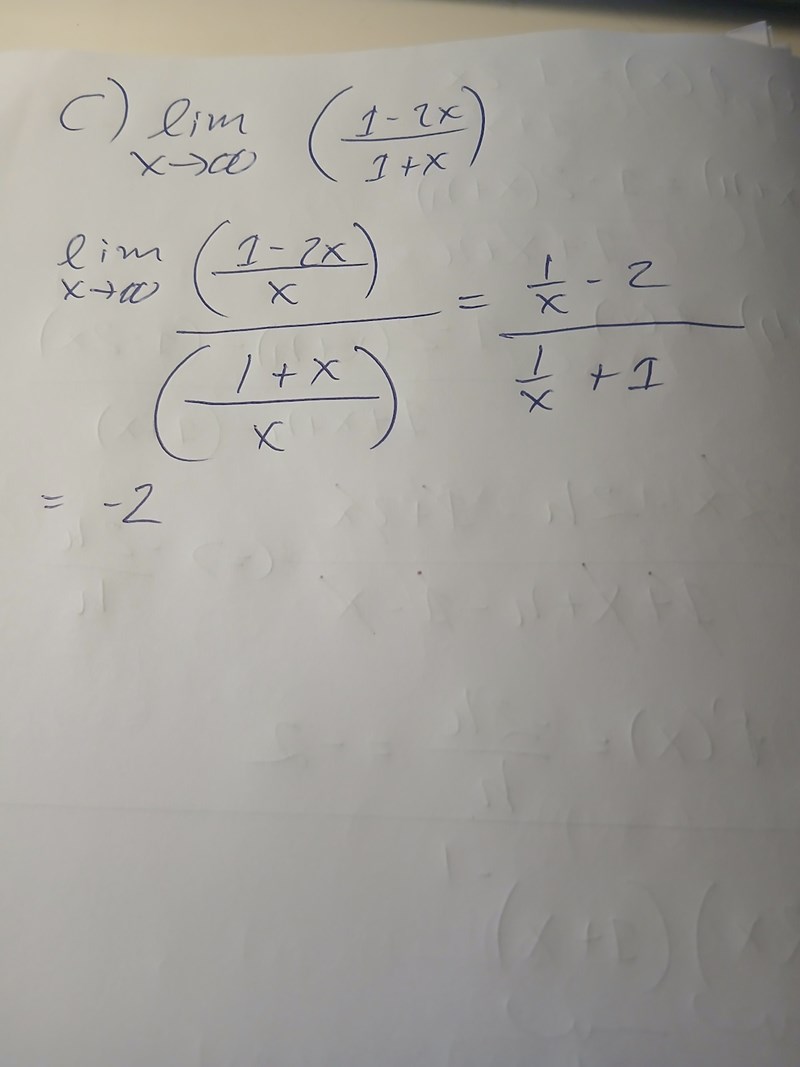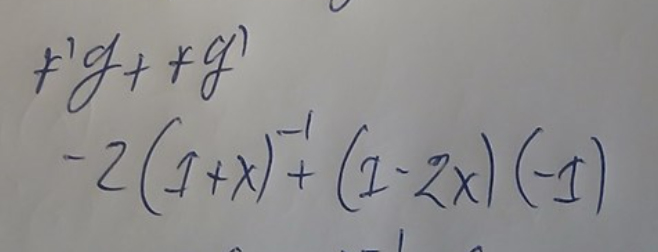3 steg derivata uppgift

Så häe hae jag tänkt
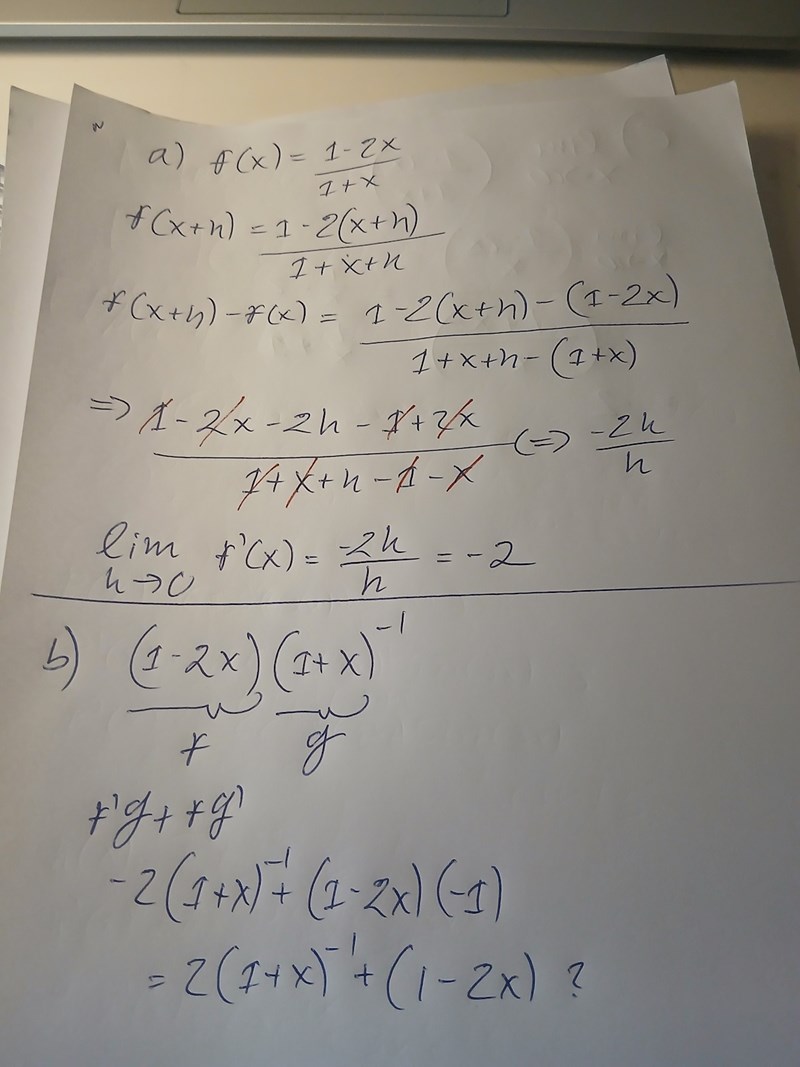
I a uppgiften, Det här ledet är fel, du måste göra liknämnigt om du ska få det på ett gemensamt bråkstreck!
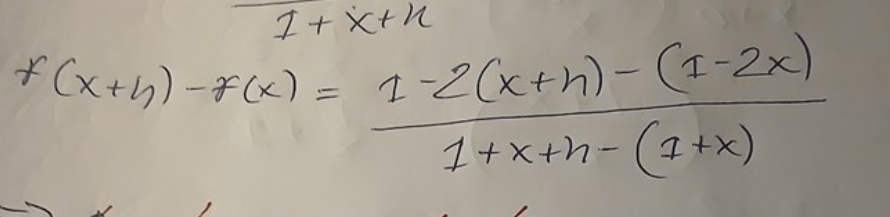
på b uppgiften gör du fel här
Derivatan av (1+x)-1 får jag till -1(1+x)-2
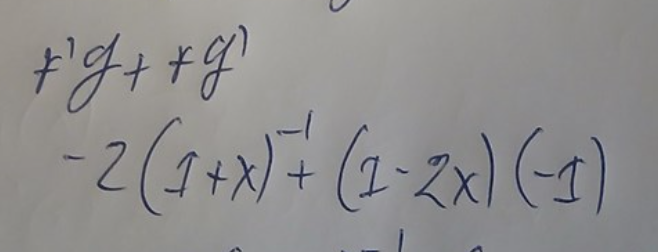
Arup skrev:
Ja, c uppgiften ser bra ut!
så hur hade rätt uppställning flr a) uppgiften varit ?
Ture skrev:på b uppgiften gör du fel här
Derivatan av (1+x)-1 får jag till -1(1+x)-2
jag du har rätt exponenten minskas med 1
Arup skrev:så hur hade rätt uppställning flr a) uppgiften varit ?
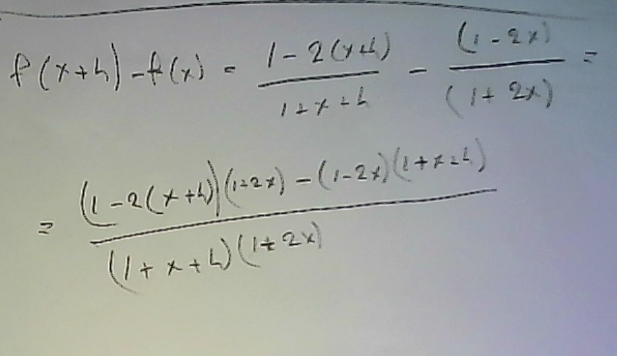
Hur gör man då på b) uppgiften ?
Arup skrev:Hur gör man då på b) uppgiften ?
Du kan visa att ekvationen f'(x) = 0 saknar (reella) lösningar. Förstår du varför det räcker?
Yngve skrev:Arup skrev:Hur gör man då på b) uppgiften ?
Du kan visa att ekvationen f'(x) = 0 saknar (reella) lösningar. Förstår du varför det räcker?
nej. Det gör jag inte
Är du med på att en funktion f(x) har stationära punkter (dvs minimi- eller maximipunkter) där derivatan är lika med 0, dvs där f'(x) = 0?
Dvs att om vi löser ekvationen f'(x) = 0 så får vi x-koordinaterna för alla stationära punkter?
Tillägg: 17 dec 2025 13:36
Även terrasspunkter är stationära punkter, se svar #20.
Den första a uppgiften blir enligt definitionen. Lite rörigt men h skall vara med i nämnaren.
f´(X) = ((1-2x-2h))/(1+x+h)-(1-2x)/(1+x))/h
= ((1-2X-2h)(1+x)-(1-2X)(1+x+h))/(h(1+x+h)(1+x))
= ...
= -3h/(h(1+x+h)(1+x))
=-3/((1+x+h)(1+x)) .... h-> 0
= -3/((1+x)(1+x))
Arup skrev:

Yngve skrev:Är du med på att en funktion f(x) har stationära punkter (dvs minimi- eller maximipunkter) där derivatan är lika med 0, dvs där f'(x) = 0?
Dvs att om vi löser ekvationen f'(x) = 0 så får vi x-koordinaterna för alla stationära punkter?
Aha ok, nu fattar jag. Ixh andra derivatan(vilket inte efterfågas) kan avgöra om funktionen är max/min ?
Arup skrev:
Aha ok, nu fattar jag.
Bra. Det betyder alltså att om ekvationen f'(x) = 0 saknar (reella) lösningar så finns det inget x-värde där funktionen har stationära punkter, vilket i sin tur innebär att funktionen saknar både minimi- och maximipunkter.
Eftersom det inte heller anges någon definitionsmängd/något intervall inom vilket vi ska söka så finns det inte heller några randpunkter som skulle kunna vara minimi- eller maximipunkter.
Ixh andra derivatan(vilket inte efterfågas) kan avgöra om funktionen är max/min ?
Ja, det stämmer. Om uppgiften hade gällt att hitta stationära punkter och avgöra deras karaktär så kunde det vara en bra idé att använda andraderivatans tecken vid de stationära punkterna.
vad innebär att en punkt är "stationär" ?
Arup skrev:vad innebär att en punkt är "stationär" ?
Läs Yngves svar #13.
Arup skrev:vad innebär att en punkt är "stationär" ?
(Utökar beskrivningen från svar #13)
En stationär punkt är en punkt där funktionens graf har en horisontell tangent, dvs där funktionens förstaderivata har värdet 0.
En stationär punkt är alltså antingen en minimi-, maximi- eller en terrasspunkt.
så här ?
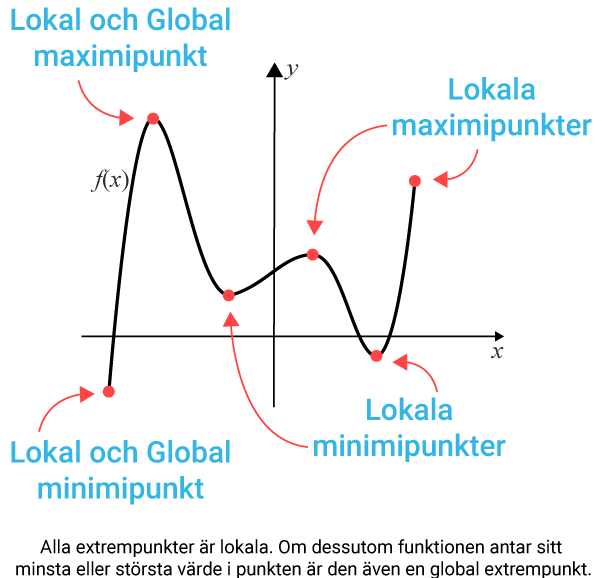
Ja, det stämmer.
Av dessa 6 punkter är det endast 4 som dessutom är stationära punkter.