4222 komplexa tal i polär form
Hej! Hur tar jag mig vidare härifrån?

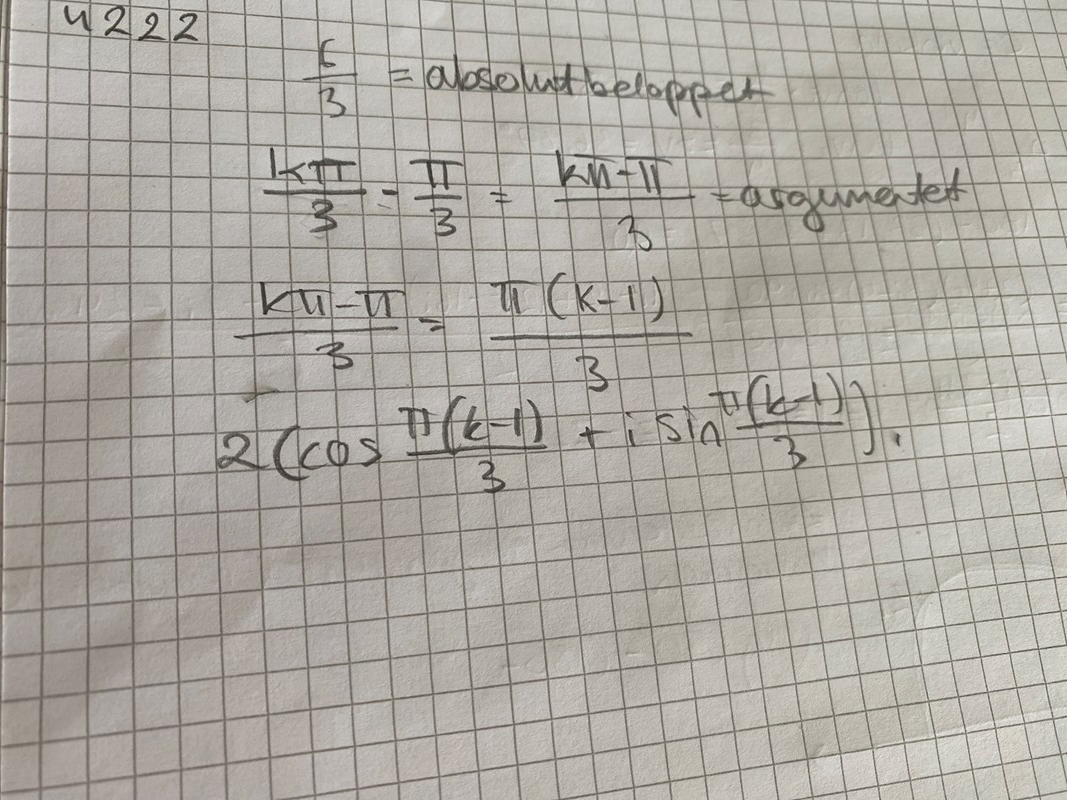
Hej.
Jättebra början.
Du vill nu bestämma det/de värden på k som gör att argumentet blir lika med argumentet för (med periodicitet ).
Nästa steg bör då vara att bestämma detta argument.
Yngve skrev:Hej.
Jättebra början.
Du vill nu bestämma det/de värden på k som gör att argumentet blir lika med argumentet för (med periodicitet ).
Nästa steg bör då vara att bestämma detta argument.
Sant. Men hur bestämmer jah argumnetwt för något i rektangulär form
Bestäm först absolutbeloppet .
Då blir talet så
Då kan man finna vinkeln. Obs att det finns hur många som helst genom multiplikation med 2 pi!
Ha en fin dag skrev:
Sant. Men hur bestämmer jah argumnetwt för något i rektangulär form
Om du vill bestämma Arg z så bör du alltid börja med att markera z i det komplexa talplanet så att du vet villen kvadrant som.är aktuell.
Sedan kan du utnyttja att tan(v) = (Im z)/(Re z)
Läs gärna mer om detta här. Fråga sedan oss om allt du vill att vi förklarar närmare.
Yngve skrev:Ha en fin dag skrev:Sant. Men hur bestämmer jah argumnetwt för något i rektangulär form
Om du vill bestämma Arg z så bör du alltid börja med att markera z i det komplexa talplanet så att du vet villen kvadrant som.är aktuell.
Sedan kan du utnyttja att tan(v) = (Im z)/(Re z)
Läs gärna mer om detta här. Fråga sedan oss om allt du vill att vi förklarar närmare.
Tack, nu löste jag!



