5 personer, 2 val vardera bland 4 alternativ
Hej, jag sitter med ett problem som jag bara inte lyckas lista ut. Jag har nämligen 5 personer som har 2 val vardera bland 4 alternativ (i detta fall bland "likvärdiga" bilmärken). Återläggning tillåts inte och ordningen spelar ingen roll.
- Ω = Jag vill beräkna utfallsrummet; på hur många sätt kan dessa bilar bli valda på enligt villkoret att vardera person endast har 2 val.
- A = Sen vill jag räkna ut på hur många sätt bilarna kan väljas på om personerna väljer slumpmässigt, alltså enl. dirichlets lådprincip så att valen fördelas så jämlikt som möjligt. Se bild nedan:
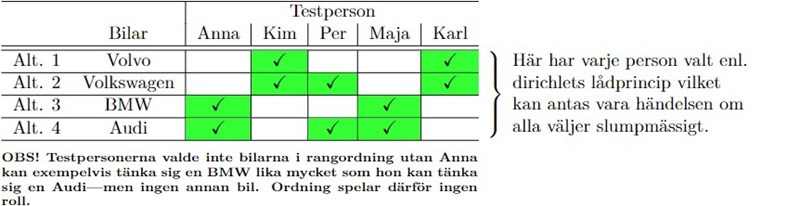
- B = Sen vill jag räkna ut på hur många sätt en bil kan bli vald ex. 5 ggr (se bild nedan). Hur dem andra bilarna blir valda i detta fall tror jag inte spelar någon roll?

P(slump)=A/Ω
P(inte slump)=B/Ω
Jag vill nämligen kunna påvisa att vissa bilmärken väljs av en anledning och inte av ren slump. Jag behöver P(slump) och P(inte slump) för att kunna använda dessa andelar i ett andelstest.
Någon som ser något samband? Tack!
Hej adi,
Vad är det du vill ha hjälp med och hur långt har du kommit? Du verkar ha gjort en del egna tolkningar av problemet. Hur ser den ursprungliga frågan ut?
Och för att komma en bit på vägen
1 person som tvingas välja exakt 2 bilmärken utan hänsyn till ordning av 4 möjliga kan göra det på möjliga vis. Hur många kombinationer kan man då framtvinga ur 5 personer?
Hej D4NIEL!
Ja, jag tänker såhär, men funderar på om detta verkligen är rätt.
Ω = = 7776
Sen för A, så tänker jag följande:
A = = 256
Varför jag har 4C1 är för att såsom Kim och Karl valt Alt. 1 (Volvo) kan ju ske på 4 olika sätt, alltså antingen hamnar deras gemensamma val på Alt. 1, Alt. 2, Alt. 3, eller Alt. 4a. Detsamma gäller ju för de andra:
Kim & Karl väljer ett bilmärke gemensamt = 4C1
Kim, Per & Karl väljer ett bilmärke gemensamt = 4C1
Anna & Maja väljer ett bilmärke gemensamt = 4C1
Anna, Per & Maja väljer ett bilmärke gemensamt = 4C1
Totalt = A = = 256
Däremot blir detta i så fall samma för B och teorin om slump kontra icke-slump faller ju... Därför måste man kanske ta hänsyn till det horisontella ledet också på något sätt? Däremot får det ju i så fall inte bli enligt nedan... Att Kim och Karls val hamnar på Anna och Maja eftersom villkoret om 2 val vardera måste vara uppfyllt...

Det finns ingen specifik fråga, detta är ett eget problem jag har för en undersökning jag gjort och vill på något sätt kunna påvisa att vissa bilar blivit valda av annan anledning än slumpen (exempelvis för Volvo i punkt 3 i inlägget).
På din fråga 1 har du tänkt rätt.
Fråga 2 är däremot fel i frågeställningen. "om personerna väljer slumpmässigt, alltså enl. dirichlets lådprincip så att valen fördelas så jämlikt som möjligt" är motsägelsefullt. Ska det vara enligt lådprincipen är det inte slumpmässigt.
Fråga 3: Hur stor är sannolikheten att Anna väljer just en Volvo? ...och så är det fem personer...
Dina kommentarer till tabellerna stämmer inte. Den första har jag redan kommenterat, och i den andra påstår du att ett utfall där alla väljer Volvo inte kan vara slumpmässigt. Det kan det ju vara.
Hej Bubo, tack för kommentaren!
För fråga 2 tänkte jag att slumpen = 0,25 x 10 val = 2,5. Att välja en bil 2,5 ggr går inte, därför måste fördelningen för att bilarna ska bli valda "slumpmässigt" bli 2x2 samt 3x2 (enl. dirichlets lådprincip, liksom "maximalt utspritt"). Stämmer inte detta? Det blir ju mer tydligt om man säger att 1000000 personer väljer slumpmässigt (utan åsikt, bara tar 2 av alternativen hej villt), då kommer det ju tillslut visa sig att det blir fördelat 25% för varje alternativ.
Absolut kan utfallet där alla väljer en Volvo ske av ren slump, men enl. en viss signifikansnivå så kanske man kan bevisa det motsatta, att det förmodligen skedde av annan anledning än slumpen.
adi1 skrev:Hej Bubo, tack för kommentaren!
För fråga 2 tänkte jag att slumpen = 0,25 x 10 val = 2,5. Att välja en bil 2,5 ggr går inte, därför måste fördelningen för att bilarna ska bli valda "slumpmässigt" bli 2x2 samt 3x2 (enl. dirichlets lådprincip, liksom "maximalt utspritt"). Stämmer inte detta? Det blir ju mer tydligt om man säger att 1000000 personer väljer slumpmässigt (utan åsikt, bara tar 2 av alternativen hej villt), då kommer det ju tillslut visa sig att det blir fördelat 25% för varje alternativ.
Absolut kan utfallet där alla väljer en Volvo ske av ren slump, men enl. en viss signifikansnivå så kanske man kan bevisa det motsatta, att det förmodligen skedde av annan anledning än slumpen.
Varifrån kommer siffrorna 0,25 respektive 10 val? Det fanns väl 4 olika bilar att välja mellan? Är det däriftån 1/4 kommer? Är det att de 5 personerna skall välja 2 bilar var, d v s 10 totalt?
Om någonting är slumpmässigt betyder det inte att valen måste ligga maximalt utspritt - det är ju inte slumpmässigt! Däremot är det så att om man har väldigt många "stickprov" så kommer resultatet att närma sig normalfördelat - men det gäller definitivt inte för 5 personer.
Hej Smaragdalena, och tack, helt fel av mig att bland in 0.25.
5 personer, 2 val vardera (tot. 10) väljer utspritt bland 4 alternativ = 10/4 = 2.5. Men ett alternativ kan inte väljas 2.5 ggr ju, därför måste fördelning bli att två alternativ väljs minst 3 ggr för "maximalt utspritt."
Om någonting är slumpmässigt betyder det inte att valen måste ligga maximalt utspritt - det är ju inte slumpmässigt! Däremot är det så att om man har väldigt många "stickprov" så kommer resultatet att närma sig normalfördelat - men det gäller definitivt inte för 5 personer.
Ja ok, det är ju sant. Men på vilket annat sätt kan slumpen i detta fall bli representerat? Kanske blir det lite tydligare om jag lägger till min hypotes:
H0: 5 matchningar sker av ren slump
H1: 5 matchningar sker av någon annan anledning
Behöver en andel för ren slump = "" = A/Ω, samt en andel för det observerade utfallet "" = B/Ω, för att kunna putta in dessa i följande testfunktion:
Sen se om
Förstår bara inte hur jag kan beräkna andelarna...
Om jag förstår din fråga, så vill du titta på de val som är gjorda, och ur det dra slutsatser om hur många personer som väljer medvetet respektive hur många som väljer slumpmässigt.
Det går inte.
Ok, tack hörrni för ert engagemang! Jag trodde det gick att statistiskt påvisa att Volvo troligtvis inte blivit vald av slumpen, utan att det med större sannolikhet fanns en anledning till varför alla mina testpersoner gemensamt valde just Volvo.
Det går.
Det är en fråga av samma typ som "Nu har jag slagit fjorton sexor i rad. Kan tärningen verkligen vara riktig?"
Ja, tärningen är inte riktig, eller så har man världens tur. Men vad har min observerade händelse för association till detta?
En riktig tärning ger fjorton sexor på fjorton kast med sannolikheten (1/6)^14
Om de fem personerna slumpmässigt väljer bilar blir sannolikheten för fem Volvo (1/2)^5
En riktig tärning ger fjorton sexor på fjorton kast med sannolikheten (1/6)^14
Juste, och till testfunktionen får man för då tänka 14/14 "rätt," med sannolikhet = 1/6. Right?
Om de fem personerna slumpmässigt väljer bilar blir sannolikheten för fem Volvo (1/2)^5
Hmm, juste, det är 2/4 för hur en person väljer bland de fyra bilmärkena genom slump, sen så sker det för varje person (^5). Och när 5 personer väljer samma bilmärke, då blir det 5 i rad, detta kan ske på olika sätt—vilket blir 4a såklart. Kan man tänka såhär då sen?
Är detta sannolikheten för en händelse där alla personer väljer minst en och samma bil?
Nä nu blir det som att du tänker att händelsen "Alla väljer Volvo" och händelsen "Alla väljer Audi" är oberoende. Det är de inte.
Under H_0: "Varje bil har samma sannolikhet att bli vald" får vi sanno att någon bil blir vald av alla 5 deltagare:
Möjliga utfall är 6^5. Gynnsamma utfall är antal utfall där Volvo blir vald av alla 5 + antal utfall där Audi blir vald av alla 5 + antal utfall där BMW väljs av alla 5 + antal utfall där VW väljs av alla 5 - antal utfall där två olika bilar väljs av alla 5.
Antal gynnsamma utfall där någon bil blir vald av alla 5 är 3^6. Antal utfall där två olika bilar väljs av alla 5 är 6 (4 choose 2). Så sanno under H_0 att någon bil väljs av alla 5 blir:
Jag tror inte det finns något som heter "välja enligt Dirichlets lådprincip". Den principen säger bara något om vad som händer ifall man lägger fler saker i lådor än man har lådor. Det är inte en princip man kan välja att följa eller inte följa.
Vi har diskuterat lite fram och tillbaka, men jag förstår fortfarande inte vad frågan egentligen är, exakt.
Den är placerad på gymnasienivå. Stämmer det?



