9 Eulers
Hej! Jag fattar inte hur jag ska lösa uppgift 9. Jag försökte följa mina anteckningar, men det blir bara väldigt komplicerat då jag går att y = 20… hur ska jag tänka?



Din början är bra.
y' = -xy-1/y stämmer.
Första raden i tabellen är rätt. Första punkten är (0; 1) och lutningen där är mycket riktigt -1.
Efterspm du till slut ska hamna vid x = -2 så ska du nu gå åt vänster med steglängd 0,05.
Nästa x-värde blir därför -0,05. Är du med på det?
Vid detta x-värde blir y-värdet 1,05. Är du med på det?
Andra punkten är alltså (-0,05; 1,05).
Lutningen vid denna punkt är y' = -(-0,05)*1,05-1/1,05 vilket är ungefär lika med -0.899880952.
Så andra raden i tabellen blir
(-0,05; 1,05) -0.899880952
Och så vidare.
tack för svar! hur fick du 1,05? satte du in x värdet i ekvationen för derivatan med derivatan -1 och löste ut y?
Nej det är från punkt 6 i din handskrivna steg-för-steg-lista.
Dvs gå en steglängd i önskad riktning med den tidigare beräknade lutningen för att komma till nästa y-värde.
jag förstår inte riktigt. Jag förstod det steget som att man ersätter y' med den tidigare riktingen och sedan satte x lika med det tidigare x värdet + steglängden
Eulers metod bygger på att man approximerar en funktionsgraf med ett antal linjesegment, där varje linjesegment från startpunkt till slutpunkt har den lutning som beräknats vid startpunkten och utsräckning i x-led som motsvarar steglängden.
Påhittat exempel:
Säg att vi utgår från den kända punkten (1: 1) där vi har beräknat derivatan till 0,5 och att vi nu vill ta reda på y-värdet vid x = 2, steglängd 0,25..
Vi ritar därför ett linjesegment med lutning 0,5 från x = 1 till x = 0,25. Det nya y-värdet blir då 1+0,25*0,5 = 1,125.
Punkt 2 blir därför.(1,25; 1,125)
Vi beräknar nu derivatan i denna punkt och kommer fram till att den är.0,4.
Nästa linjesegment går då från (1,25; 1,125) till (1,25+9,25; 1,125+0,25*0,4) = (1,5; 1,225)
Och så vidare.
Blev det tydligare då?
Kolla gärna denna genomgång som förklarar metoden på.ett bra sätt.
Det enda som inte stämmer med din uppgift är att vi där måste gå baklänges i x-led vilket han i videon säger att man normalt inte gör.
Yngve skrev:Kolla gärna denna genomgång som förklarar metoden på.ett bra sätt.
Det enda som inte stämmer med din uppgift är att vi där måste gå baklänges i x-led vilket han i videon säger att man normalt inte gör.
Ah, det är den där läraren som tidigare myntade "Jag vet inte varför det är så, men det är det".
Här kör han, ett par sekunder in, med den mycket motiverande frasen "Det kan komma på ett prov" som motivering varför det kan vara bra att känna till Eulers metod, inte att det är en viktig metod i sig för approximering. Vilken härlig nivå han ligger på. Tur man inte hade en sådan lärare.
Yngve skrev:Eulers metod bygger på att man approximerar en funktionsgraf med ett antal linjesegment, där varje linjesegment från startpunkt till slutpunkt har den lutning som beräknats vid startpunkten och utsräckning i x-led som motsvarar steglängden.
Påhittat exempel:
Säg att vi utgår från den kända punkten (1: 1) där vi har beräknat derivatan till 0,5 och att vi nu vill ta reda på y-värdet vid x = 2, steglängd 0,25..
Vi ritar därför ett linjesegment med lutning 0,5 från x = 1 till x = 0,25. Det nya y-värdet blir då 1+0,25*0,5 = 1,125.
Punkt 2 blir därför.(1,25; 1,125)
Vi beräknar nu derivatan i denna punkt och kommer fram till att den är.0,4.
Nästa linjesegment går då från (1,25; 1,125) till (1,25+9,25; 1,125+0,25*0,4) = (1,5; 1,225)
Och så vidare.
Blev det tydligare då?
hmm jaha, då har jag missuppfattat metoden helt. jag tänkte att man använde uttrycket för derivatan för att beräkna det nya värdet. så i mitt fall är det y´ = -xy - (1/y) vilket ger -1 = -(-0,05)y - (1/y). Är det alltid så att man tar x-värdet + steglängden x den ursprungliga derivatan för att få fram det nya y-värdet?
Trinity2 skrev:Yngve skrev:Kolla gärna denna genomgång som förklarar metoden på.ett bra sätt.
Det enda som inte stämmer med din uppgift är att vi där måste gå baklänges i x-led vilket han i videon säger att man normalt inte gör.
Ah, det är den där läraren som tidigare myntade "Jag vet inte varför det är så, men det är det".
Här kör han, ett par sekunder in, med den mycket motiverande frasen "Det kan komma på ett prov" som motivering varför det kan vara bra att känna till Eulers metod, inte att det är en viktig metod i sig för approximering. Vilken härlig nivå han ligger på. Tur man inte hade en sådan lärare.
jag tycker det är det som gör honom pedagogisk. Han förklarar saker simpelt och tydligt, utan massa tillägg, men ändå så man förstår
Ha en fin dag skrev:
[...]
Är det alltid så att man tar x-värdet + steglängden x den ursprungliga derivatan för att få fram det nya y-värdet?
Nej, man tar y-värdet plus steglängden gånger derivatan för att få det nya y-värdet.
(Fast i din uppgift så blir det öite annorlunda eftersom du ska gå i negativ x-riktning).
Om du ritar ett koordinatsystem och använder metoden i det så kommer du att se hur det hänger ihop.
Fråga gärna här om inte polletten trillar ner.
Man kan hålla uppgiften ganska analytisk och få en rekursionsformel, men det kanske inte är mening med uppgiften.
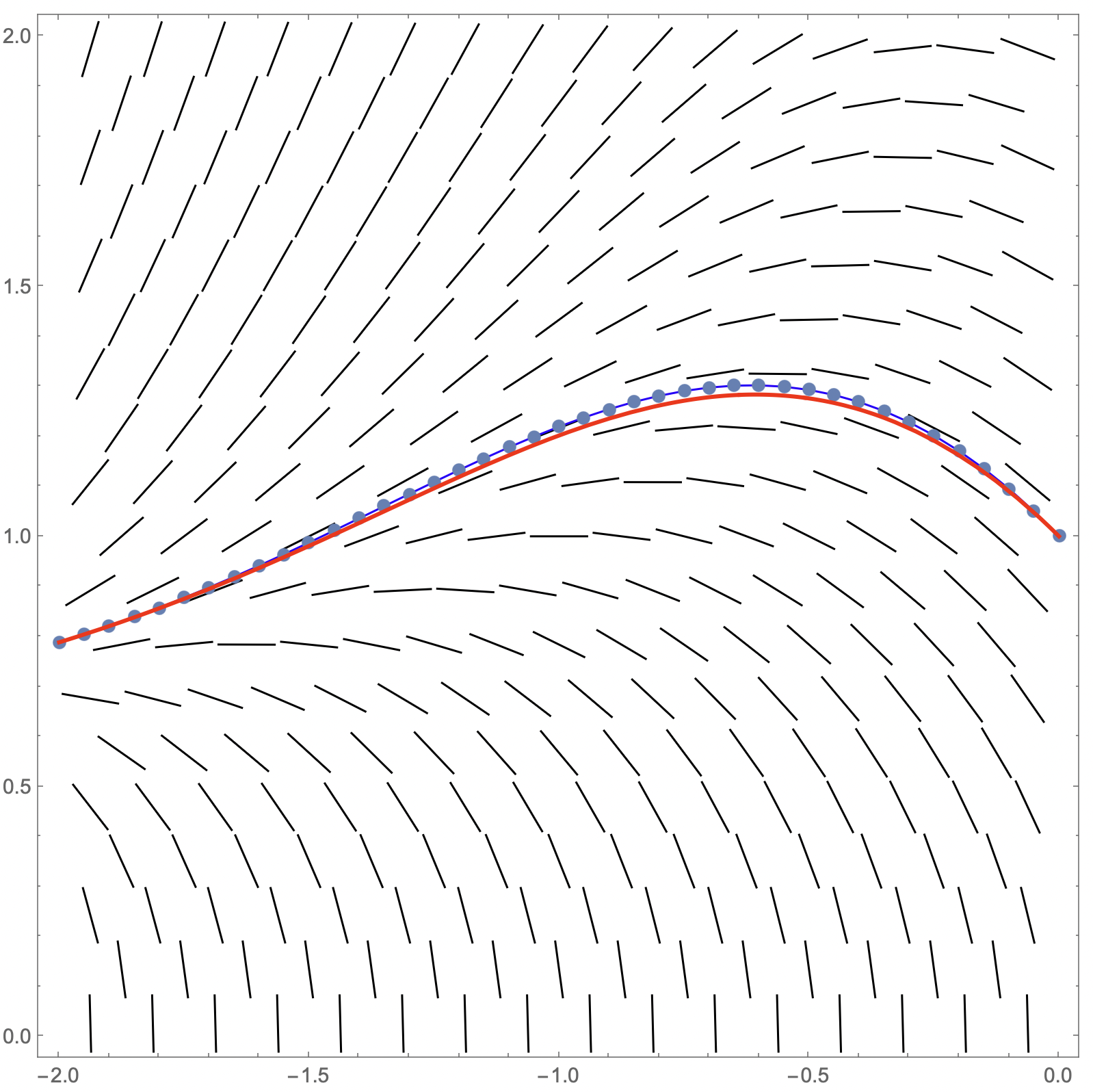
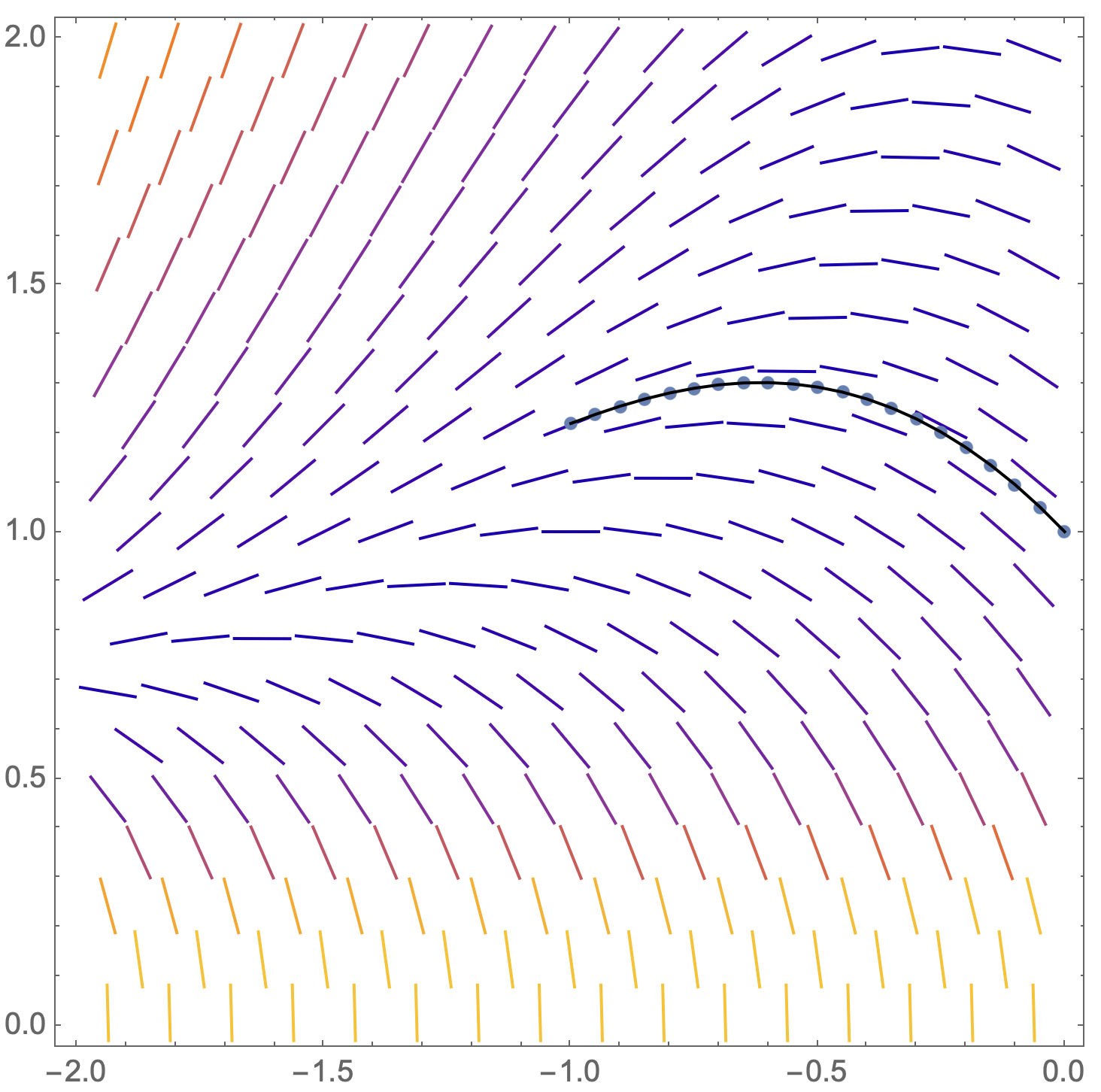
Det blir intensiva beräkningar, även i Mathematica, där jag bara orkade med att vänta på 20 steg, upp till -1. Rekursion är inte M's starka sida. Kanske Python är bättre. Men det blir snygga figurer, t.ex. i kombination med riktningsfältet.
Något förbättrad graf. Den röda grafen är den exakta lösningen.